这一周我们将学习到如何利用 CNN 进行图片风格转换和人脸识别。

人脸识别

什么是人脸识别或人脸校验

• 人脸校验
  • 输出图片，姓名或身份号
  • 输出是否输入图片是对应的那个人
  • 这是一个 1：1 问题
• 人脸识别
  • 有 K 个人的数据库
  • 输入图片
  • 输出这个人的 ID 号，如果它是这 K 个人之一的话，如果不是，输出“未识别”
  • 这是一个 1：K 问题

单样本学习 one-shot learning

单样本学习指的是用一张样本照片进行学习，然后再次识别出这个人。由于只有一个样本，所以如果直接输入到 CNN 进行训练，效果非常不好。

正确的做法是学习出一个“相似度”函数 d(img1, img2)，它等于两个图片的不同程度，如果 $d(img1, img2) \le \tau$，那么这两张图片就是一个人，如果反之，这不是一个人。

孪生网络 Siamese network

[Taigman et. al., 2014. DeepFace closing the gap to human level performance]

假设我们有两张图片 $x^{(1)}, x^{(2)}$，我们将它们通过一个卷积网络，输出两个编码向量 $f(x^{(1)})$ 和 $f(x^{(2)})$，训练这个网络，使得我们确信这个编码是对这两张图片的良好表达，这个相似度函数就是两张照片的编码的差的范数。

$$d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||^2_2$$

这个概念被称作孪生网络。

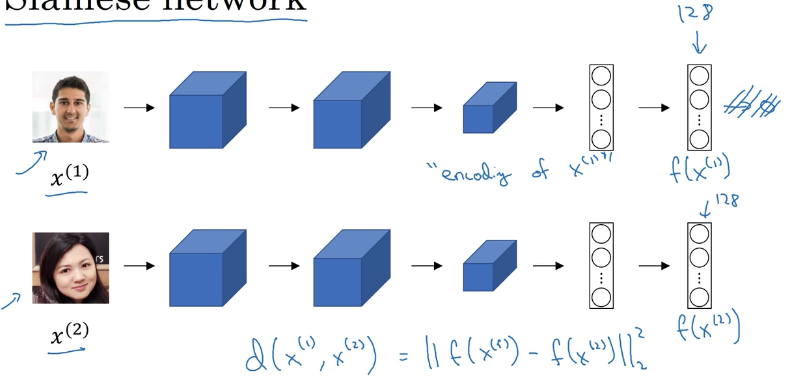
如何训练？

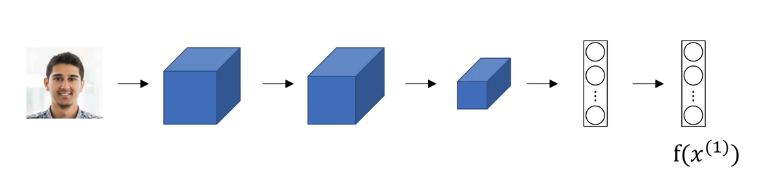
• 神经网络的参数定义了图片的一个编码 $f(x^{(i)})$
• 学习参数使得：
  • 如果 $x^{(i)}$ 和 $x^{(j)}$ 是同一个人，那么 $||f(x^{(1)})-f(x^{(2)})||^2_2$ 就很小
  • 如果 $x^{(i)}$ 和 $x^{(j)}$ 是不同的人，那么 $||f(x^{(1)})-f(x^{(2)})||^2_2$ 就很大

三元损失函数 Triple Loss

引例

首先我们有一个“锚 Anchor”照片 A，如果另一张照片和这个锚照片是同一个人，着称之为“正例 Positive” P，反之称为“反例 Negative” N，如下图所示：

我们期望的是 A 和 P 的差距 d(A, P) 要小于 A 和 N 的差距 d(A, N)，即：

$$d(A, P) \le d(A,N) \\ ||f(A)-f(P)||^2 \le ||f(A)-f(N)||^2\\ ||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 \le 0$$

但是为了防止神经网络把 f(A) 和 f(P) 和 f(N) 训练得特别接近，例如当它们都为 0 时，上式仍然满足，为了防止神经网络输出退化解，增大 d(A, P) 和 d(A, N) 之间的差距，我们增加一个超参数 margin $\alpha$，式子变成：

$$d(A, P) + \alpha \le d(A,N) \\ ||f(A)-f(P)||^2 + \alpha \le ||f(A)-f(N)||^2 \\ ||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 + \alpha \le 0$$

当 d(A, P) = 0.5 时，加上 $\alpha$ = 0.2，则 d(A, N) 至少为 0.7，使得 d(A, P) 远小于 d(A, N)。

三元损失函数定义

给定三个图片 A，P，N：

$$L(A,P,N)=max(||f(A)-f(P)||^2 - ||f(A)-f(N)||^2 + \alpha, \ 0 )$$

总的代价函数为：

$$J = \sum\limits ^m_{i=1}L(A^{(i)},P^{(i)},N^{(i)})$$

我们必须保证每个人不止一张照片，假设训练集为 1000 个人的 10000 张照片，我们需要拿这 10000 张照片去生成上式的三元组。

如何选择三元组 A, P, N

在训练时，如果你随意选择 A，P，N，那么 $d(A, P) + \alpha \le d(A,N)$ 这个式子会非常容易满足，因为如果随便挑的 d(A, P) 会有很大几率远小于 d(A, N)，这样导致神经网络无法从中学到东西。

我们需要做的是挑选那种很难训练的三元组，使得你挑的 A, P, N 会让 d(A,P) 很靠近 d(A,N)，这样使得算法在学习的时候要花更多的力气尝试让右边这一项增大，左边这项减小，也就是使得：

$$d(A, P) \approx d(A, N)$$

更多三元组选择方法见这篇论文。

人脸识别的二元分类方法

除了三元损失函数，我们还有其他的定义损失函数的方法。

$$\hat y = \sigma (\sum\limits ^{128} _{k=1}w_i|f(x^{(i)})_k-f(x^{(j)})_k|+b)$$

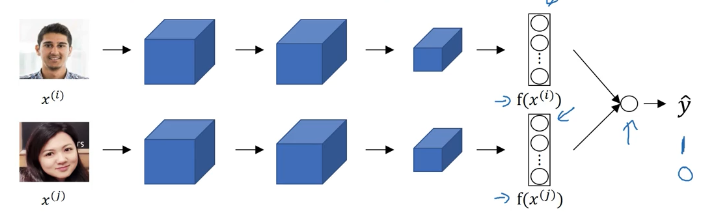
还有一种变种 $\chi ^2$ 相似度：

$$\hat y = \sigma (\sum\limits ^{128} _{k=1}w_i \frac{(f(x^{(i)})_k-f(x^{(j)})_k)^2}{f(x^{(i)})_k+f(x^{(j)})_k} +b)$$

一个小技巧是我们不必每次都计算数据库中的图片的编码值，我们可以先进行预计算，在进行识别时直接跟这些预计算的编码值进行比较，然后预测结果 y.

神经风格转化 Neural style transfer

什么是神经风格转化

深度卷积网络的可视化

假设我们正在训练这样一个网络：

为了知道每一层到底在计算什么，并将其可视化，我们可以在这层挑出一个神经元，找到使得这个神经元激活值最大的九个图像小块。在更深的层，隐藏单元能看到更大一部分图像，即更大图像对这些层的输出有影响，我们将每一层可视化，如下图所示。

我们可以看到，第一层在检测一些边缘特征，随着层数的加深，检测的对象越来越复杂。

代价函数

[Gatys et al., 2015. A neural algorithm of artistic style. Images on slide generated by Justin Johnson]

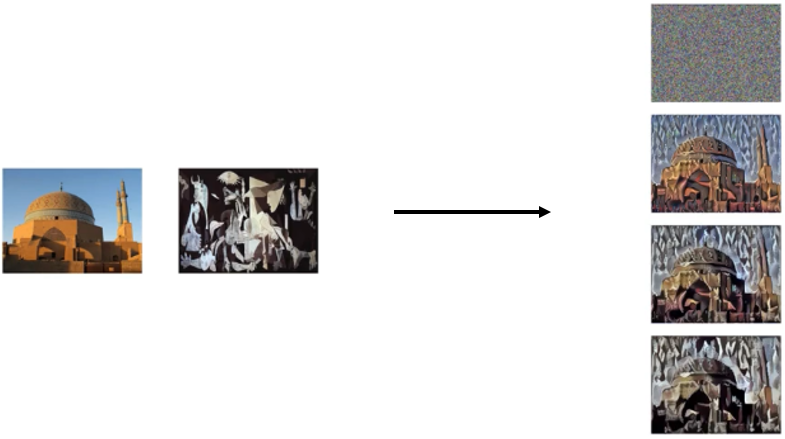
问题的形式是：我们有一张“内容 content 图片” C，一张“风格 style 图片” S，得到一个“生成 generated 图像” G。我们需要一个代价函数 J(G) 来评价某个图像生成的质量有多好，用梯度下降使得 G 的损失最小，从而生成想要的图像。

代价函数分为两部分： 内容代价函数，表示生成图像和内容图像之间的相似程度，以及风格代价函数，表示生成图像和风格图像之间的相似程度，再加上两个系数表示风格代价和内容代价之间的比重。

$$J(G)= \alpha J_{content}(C,G)+\beta J_{style}(S,G)$$

如何生成 G：

• 将 G 随机初始化
  • G : 100×100×3
• 使用梯度下降最小化 J(G)
  • $G:=G- \frac{\partial J(G)}{\partial G}$ 不同于更新权重，我们通过梯度下降更新 G 的像素值来最小化 J(G)

内容代价函数

$$J(G)= \alpha J_{content}(C,G)+\beta J_{style}(S,G)$$

• 假设使用 $l$ 个隐藏层来计算内容代价函数
• 使用预训练的卷积网络，比如 VGG 网络
• 分别将内容图片 C 和生成图片 G 输入这个网络，假设 $a ^ { [ l ] ( C ) }$ 和 $a ^ { [ l ] ( G ) }$ 分别是第 $l$ 层的内容图像 C 和生成图片 G 的激活值
• 如果 $a ^ { [ l ] ( C ) }$ 和 $a ^ { [ l ] ( G ) }$ 很接近，那么两张图片就有相似的内容，所以内容代价函数为：

$$J_{content}(C,G) = \frac{1}{2}||a ^ { [ l ] ( C ) } - a ^ { [ l ] ( G ) }||^2$$

风格代价函数

如何定义一张图片的“风格”

假设我们使用方框框起来的那一层的激活值来测量“风格”，我们把“风格”定义为这一层的激活值的不同通道之间的相关性。

关于图片风格的解释

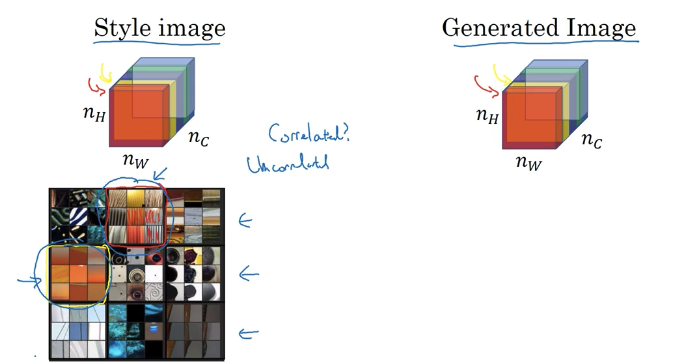
假设红色通道表示红框框起来的特征（那些竖条纹），黄色通道表示黄框框起来的特征（即那些橘红色的图块），那么，红色通道和黄色通道的相关性，可以告诉你在图片中这种竖条纹和橘色图块是否经常同时出现，这是“风格”的一种衡量方式。

风格矩阵

我们需要过给定的图像计算出风格矩阵，风格矩阵会记录上一张幻灯片中我们提到的所有相关性。

• $a^{[l]}_{i,j,k}$ 是第 $l$ 层在（i, j, k）这个位置的激活值，i 是高度，j 是宽度，k 是通道
• $G^{[l]}$ 是形状为 $n^{[l]}_c×n^{[l]}_c$ 的风格矩阵，$n^{[l]}_c$ 是第 l 层的通道数

$$风格图片的风格矩阵 \ G^{[l](S)}_{kk'}=\sum\limits^{n^{[l]}_H}_{i=1}\sum\limits^{n^{[l]}_W}_{j=1}a^{[l](S)}_{i,j,k}a^{[l](S)}_{i,j,k'}$$ $$生成图片的风格矩阵 \ G^{[l](G)}_{kk'}=\sum\limits^{n^{[l]}_H}_{i=1}\sum\limits^{n^{[l]}_W}_{j=1}a^{[l](G)}_{i,j,k}a^{[l](G)}_{i,j,k'}$$

• kk’ 表示第 k 个通道和第 k‘ 个通道的相关性，在风格矩阵的第 k 行第 k’ 列
• 线性代数中 G 矩阵被称为格拉姆矩阵 gram matrix

风格代价函数

$$J _ { \text { style } } ^ { [ l ] } ( S , G ) =\frac { 1 } { \left( 2 n _ { H } ^ { [ l ] } n _ { W } ^ { [ l ] } n _ { C } ^ { [ l ] } \right) ^ { 2 } }||G^{[l](S)}-G^{[l](G)}||^2_F \\ = \frac { 1 } { \left( 2 n _ { H } ^ { [ l ] } n _ { W } ^ { [ l ] } n _ { C } ^ { [ l ] } \right) ^ { 2 } } \sum _ { k } \sum _ { k ^ { \prime } } \left( G _ { k k ^ { \prime } } ^ { [ l ] ( S ) } - G _ { k k ^ { \prime } } ^ { [ l ] ( G ) } \right)^2$$

• $\frac { 1 } { \left( 2 n _ { H } ^ { [ l ] } n _ { W } ^ { [ l ] } n _ { C } ^ { [ l ] } \right) ^ { 2 } }$ 是不重要的标准化系数

如果我们需要将不同层的风格代价函数都考虑进去，那么式子变成：

$$J _ { \text { style } } ( S , G ) = \sum\limits _l \lambda^{[l]}J _ { \text { style } } ^ { [ l ] } ( S , G )$$

• $\lambda$ 为一个可调整的超参数

1D 和 3D 卷积

2D 到 1D 的推广

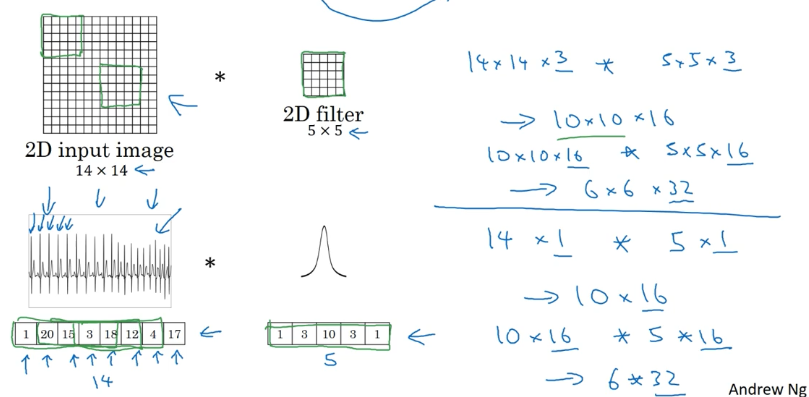
2D 到 3D 的推广