艺琛的 Livehouse主页学习笔记读书观影笔记个人随想爱好和生活相册所有博客特色标签关于我
coursera 吴恩达深度学习 Specialization 编程作业（course 4 week 2）
|学习笔记

Keras 教程

  • Keras 是一个高级神经网络框架，用 Python 写成，在 TensorFlow 和 CNTK 等一些更低级的框架上运行，拥有比 tensorflow 更高的抽象
  • Keras 能够快速搭建和试验不同的模型
  • Keras 比低级框架限制更多，无法实现一些非常复杂的模型，但是对一些普通模型运行很好

这里用 Keras 实现一个识别图片中的人是否开心的算法。

先引入我们需要的包：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
from keras import layers
from keras.layers import Input, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D
from keras.layers import AveragePooling2D, MaxPooling2D, Dropout, GlobalMaxPooling2D, GlobalAveragePooling2D
from keras.models import Model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from kt_utils import *

import keras.backend as K
K.set_image_data_format('channels_last')
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow

%matplotlib inline

加载数据集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.

# Reshape
Y_train = Y_train_orig.T
Y_test = Y_test_orig.T

print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))

在 Keras 中训练测试模型有四个步骤：

  • 建立模型

    • 自己定义一个 model() 函数进行前向传播

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      def HappyModel(input_shape):
          """
          Implementation of the HappyModel.
          
          Arguments:
          input_shape -- 输入图片的维度（不包括图片的数量！）

          Returns:
          model -- a Model() instance in Keras
          """
          X_input = Input(input_shape)

          # Zero-Padding: pads the border of X_input with zeroes
          X = ZeroPadding2D((3, 3))(X_input)

          # CONV -> BN -> RELU Block applied to X
          X = Conv2D(32, (7, 7), strides = (1, 1), name = 'conv0')(X)
          X = BatchNormalization(axis = 3, name = 'bn0')(X)
          X = Activation('relu')(X)

          # MAXPOOL
          X = MaxPooling2D((2, 2), name='max_pool')(X)

          # FLATTEN X (means convert it to a vector) + FULLYCONNECTED
          X = Flatten()(X)
          X = Dense(1, activation='sigmoid', name='fc')(X)

          # Create model. This creates your Keras model instance, you'll use this instance to train/test the model.
          model = Model(inputs = X_input, outputs = X, name='HappyModel')

          return model
      1
      happyModel = HappyModel(X_train.shape[1:])

  • 编译模型

    • model.compile(optimizer = “…”, loss = “…”, metrics = [“accuracy”])

      1
      happyModel.compile(optimizer = 'Adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

  • 在训练数据上训练模型

    • model.fit(x = …, y = …, epochs = …, batch_size = …)

      1
      happyModel.fit(x = X_train, y = Y_train, epochs = 40, batch_size = 16)

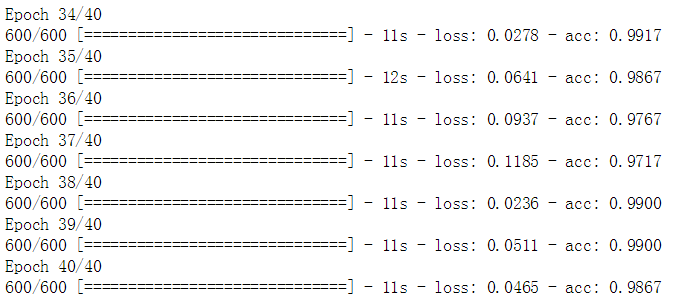
  • 在测试数据上测试模型

    • model.evaluate(x = …, y = …)

      1
      2
      3
      4
      preds = happyModel.evaluate(x = X_test, y = Y_test)
      print(preds)
      print ("Loss = " + str(preds[0]))
      print ("Test Accuracy = " + str(preds[1]))

最后可以达到 98% 的训练集精确度，90% 的训练集精确度。

我们可以用自己的图片进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
img_path = 'images/45.jpg'	# 用自己的图片路径

img = image.load_img(img_path, target_size=(64, 64))
imshow(img)

x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)

print(happyModel.predict(x))
if happyModel.predict(x) == 0:
    print('这个人不开心哦 :(')
else:
    print('这个人在笑哦 :)')

我们还可以获得模型的概况：

1
happyModel.summary()

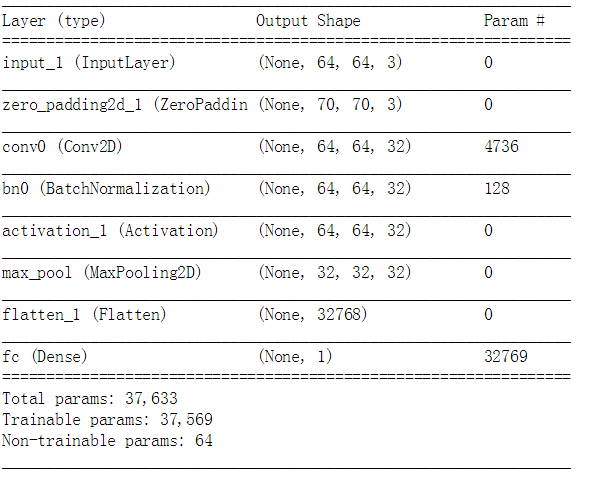
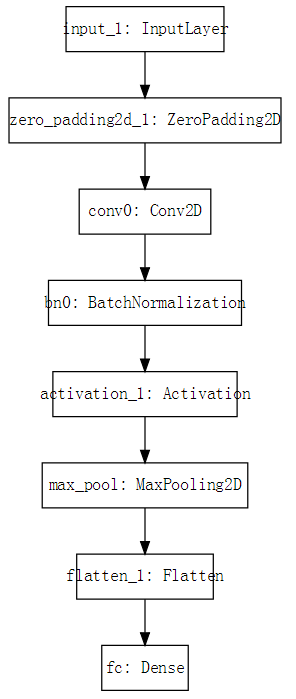
还可以将模型流程图打印出来并保存为位图文件：

1
2
plot_model(happyModel, to_file='HappyModel.png')
SVG(model_to_dot(happyModel).create(prog='dot', format='svg'))

用 Keras 创建 ResNet 残差网络

这节会用残差网络创建一个非常深的卷积网络。

  • 实现基本的残差网络组块
  • 将这些组块合在一起实现一个最先进的神经网络图像分类器

包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from resnets_utils import *
from keras.initializers import glorot_uniform
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline

import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)

非常深的神经网络的问题所在

  • 优点：很深的网络能学习到非常多层次的抽象特征，从边缘到复杂特征。
  • 缺点：训练时会产生梯度下降，使得训练速度极慢。

残差网络的基本 block 组块

有两种主要的组块在残差网络中，取决于输入/输出维度是否相同。

  1. The identity block （输入/输出维度相同）

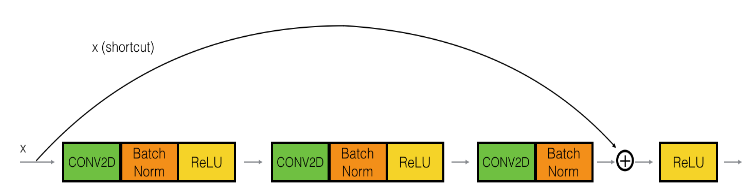
    First component of main path:

    • The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (1,1). Its padding is “valid” and its name should be conv_name_base + '2a'. Use 0 as the seed for the random initialization.
    • The first BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2a'.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    Second component of main path:

    • The second CONV2D has $F_2$ filters of shape $(f,f)$ and a stride of (1,1). Its padding is “same” and its name should be conv_name_base + '2b'. Use 0 as the seed for the random initialization.
    • The second BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2b'.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    Third component of main path:

    • The third CONV2D has $F_3$ filters of shape (1,1) and a stride of (1,1). Its padding is “valid” and its name should be conv_name_base + '2c'. Use 0 as the seed for the random initialization.
    • The third BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2c'. Note that there is no ReLU activation function in this component.

    Final step:

    • The shortcut and the input are added together.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    实现代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    # The identity block 函数
    def identity_block(X, f, filters, stage, block):
        """
        Implementation of the identity block as defined in Figure 3
        
        Arguments:
        X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
        f -- integer, specifying the shape of the middle CONV's window for the main path
        filters -- python list of integers, defining the number of filters in the CONV layers of the main path
        stage -- integer, used to name the layers, depending on their position in the network
        block -- string/character, used to name the layers, depending on their position in the network
        
        Returns:
        X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
        """
        
        # defining name basis
        conv_name_base = 'res' + str(stage) + block + '_branch'
        bn_name_base = 'bn' + str(stage) + block + '_branch'
        
        # Retrieve Filters
        F1, F2, F3 = filters
        
        # Save the input value. You'll need this later to add back to the main path. 
        X_shortcut = X
        
        # First component of main path
        X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
        X = Activation('relu')(X)
        
        # Second component of main path 
        X = Conv2D(filters = F2, kernel_size = (f,f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
        X = Activation('relu')(X)

        # Third component of main path 
        X = Conv2D(filters = F3, kernel_size = (1,1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2c' )(X)

        # Final step: Add shortcut value to main path, and pass it through a RELU activation 
        X = Add()([X,X_shortcut])
        X = Activation("relu")(X)
     
        return X

    最后的 X 加上 X_shoutcut 应该使用 Keras 内置的 Add()([]) 函数，否则后面会报错：’Tensor’ object has no attribute ‘_keras_history’

  2. The convolutional block（输入/输出维度不相同）

    当输入输出维度不相同时，在 shourtcut 这条路径使用一个卷积操作来使得维度相同。

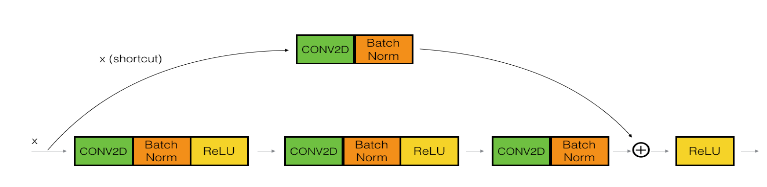
    各层的细节：

    First component of main path:

    • The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (s,s). Its padding is “valid” and its name should be conv_name_base + '2a'.
    • The first BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2a'.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    Second component of main path:

    • The second CONV2D has $F_2$ filters of (f,f) and a stride of (1,1). Its padding is “same” and it’s name should be conv_name_base + '2b'.
    • The second BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2b'.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    Third component of main path:

    • The third CONV2D has $F_3$ filters of (1,1) and a stride of (1,1). Its padding is “valid” and it’s name should be conv_name_base + '2c'.
    • The third BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '2c'. Note that there is no ReLU activation function in this component.

    Shortcut path:

    • The CONV2D has $F_3$ filters of shape (1,1) and a stride of (s,s). Its padding is “valid” and its name should be conv_name_base + '1'.
    • The BatchNorm is normalizing the channels axis. Its name should be bn_name_base + '1'.

    Final step:

    • The shortcut and the main path values are added together.
    • Then apply the ReLU activation function. This has no name and no hyperparameters.

    实现的代码为：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    # The convolutional block 函数
    def convolutional_block(X, f, filters, stage, block, s = 2):
        """
        Implementation of the convolutional block as defined in Figure 4
        
        Arguments:
        X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
        f -- integer, specifying the shape of the middle CONV's window for the main path
        filters -- python list of integers, defining the number of filters in the CONV layers of the main path
        stage -- integer, used to name the layers, depending on their position in the network
        block -- string/character, used to name the layers, depending on their position in the network
        s -- Integer, specifying the stride to be used
        
        Returns:
        X -- output of the convolutional block, tensor of shape (n_H, n_W, n_C)
        """
        
        # defining name basis
        conv_name_base = 'res' + str(stage) + block + '_branch'
        bn_name_base = 'bn' + str(stage) + block + '_branch'
        
        # Retrieve Filters
        F1, F2, F3 = filters
        
        # Save the input value
        X_shortcut = X

        ##### MAIN PATH #####
        # First component of main path 
        X = Conv2D(F1, (1, 1), strides = (s,s), name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
        X = Activation('relu')(X)

        # Second component of main path
        X = Conv2D(F2, (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
        X = Activation('relu')(X)

        # Third component of main path 
        X = Conv2D(F3, (1, 1), strides = (1,1), name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
        X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)

        ##### SHORTCUT PATH ####
        X_shortcut = Conv2D(F3, (1,1), strides = (s,s), name = conv_name_base + '1', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
        X_shortcut = BatchNormalization(axis = 3, name = bn_name_base + '1' )(X_shortcut)

        # Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
        X = X = Add()([X,X_shortcut])
        X = Activation('relu')(X)
        
        return X

建立一个 50 层的残差网络模型

这个模型的细节为：

  • Zero-padding pads the input with a pad of (3,3)
  • Stage 1:
    • The 2D Convolution has 64 filters of shape (7,7) and uses a stride of (2,2). Its name is “conv1”.
    • BatchNorm is applied to the channels axis of the input.
    • MaxPooling uses a (3,3) window and a (2,2) stride.
  • Stage 2:
    • The convolutional block uses three set of filters of size [64,64,256], “f” is 3, “s” is 1 and the block is “a”.
    • The 2 identity blocks use three set of filters of size [64,64,256], “f” is 3 and the blocks are “b” and “c”.
  • Stage 3:
    • The convolutional block uses three set of filters of size [128,128,512], “f” is 3, “s” is 2 and the block is “a”.
    • The 3 identity blocks use three set of filters of size [128,128,512], “f” is 3 and the blocks are “b”, “c” and “d”.
  • Stage 4:
    • The convolutional block uses three set of filters of size [256, 256, 1024], “f” is 3, “s” is 2 and the block is “a”.
    • The 5 identity blocks use three set of filters of size [256, 256, 1024], “f” is 3 and the blocks are “b”, “c”, “d”, “e” and “f”.
  • Stage 5:
    • The convolutional block uses three set of filters of size [512, 512, 2048], “f” is 3, “s” is 2 and the block is “a”.
    • The 2 identity blocks use three set of filters of size [512, 512, 2048], “f” is 3 and the blocks are “b” and “c”.
  • The 2D Average Pooling uses a window of shape (2,2) and its name is “avg_pool”.
  • The flatten doesn’t have any hyperparameters or name.
  • The Fully Connected (Dense) layer reduces its input to the number of classes using a softmax activation. Its name should be 'fc' + str(classes).

实现代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# 50 层的残差网络模型
def ResNet50(input_shape = (64, 64, 3), classes = 6):
    """
    Implementation of the popular ResNet50 the following architecture:
    CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
    -> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> TOPLAYER

    Arguments:
    input_shape -- shape of the images of the dataset
    classes -- integer, number of classes

    Returns:
    model -- a Model() instance in Keras
    """
    
    # Define the input as a tensor with shape input_shape
    X_input = Input(input_shape)
    
    # Zero-Padding
    X = ZeroPadding2D((3, 3))(X_input)
    
    # Stage 1
    X = Conv2D(64, (7, 7), strides = (2, 2), name = 'conv1', kernel_initializer = glorot_uniform(seed=0))(X) #  kernel_initializer = glorot_uniform 表示 Xavier 均匀初始化
    X = BatchNormalization(axis = 3, name = 'bn_conv1')(X)
    X = Activation('relu')(X)
    X = MaxPooling2D((3, 3), strides=(2, 2))(X)

    # Stage 2
    X = convolutional_block(X, f = 3, filters = [64, 64, 256], stage = 2, block='a', s = 1)
    X = identity_block(X, 3, [64, 64, 256], stage=2, block='b')
    X = identity_block(X, 3, [64, 64, 256], stage=2, block='c')

    # Stage 3 
    X = convolutional_block(X, f = 3, filters = [128,128,512], stage = 3, block = 'a', s = 2 )
    X = identity_block(X, 3, [128, 128, 512], stage = 3, block='b')
    X = identity_block(X, 3, [128, 128, 512], stage = 3, block='c')
    X = identity_block(X, 3, [128, 128, 512], stage = 3, block='d')

    # Stage 4
    X = convolutional_block(X, f = 3, filters = [256,256,1024], stage = 4, block = 'a', s = 2 )
    X = identity_block(X, 3, [256,256,1024], stage = 4, block='b')
    X = identity_block(X, 3, [256,256,1024], stage = 4, block='c')
    X = identity_block(X, 3, [256,256,1024], stage = 4, block='d')
    X = identity_block(X, 3, [256,256,1024], stage = 4, block='e')
    X = identity_block(X, 3, [256,256,1024], stage = 4, block='f')

    # Stage 5 
    X = convolutional_block(X, f = 3, filters = [512,512,2048], stage = 5, block = 'a', s = 2 )
    X = identity_block(X, 3, [512,512,2048], stage = 5, block='b')
    X = identity_block(X, 3, [512,512,2048], stage = 5, block='c')

    # AVGPOOL
    X = AveragePooling2D((2,2), name = 'avg_pool')(X)
   
    # output layer
    X = Flatten()(X)
    X = Dense(classes, activation='softmax', name='fc' + str(classes), kernel_initializer = glorot_uniform(seed=0))(X)	#  kernel_initializer = glorot_uniform 表示 Xavier 均匀初始化
    
    # Create model
    model = Model(inputs = X_input, outputs = X, name='ResNet50')

    return model

进行训练和预测

  • 建立模型

    1
    model = ResNet50(input_shape = (64, 64, 3), classes = 6)

  • 编译模型

    1
    model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

  • 训练模型

    • 载入数据

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

      # Normalize image vectors
      X_train = X_train_orig/255.
      X_test = X_test_orig/255.

      # Convert training and test labels to one hot matrices
      Y_train = convert_to_one_hot(Y_train_orig, 6).T
      Y_test = convert_to_one_hot(Y_test_orig, 6).T

      print ("number of training examples = " + str(X_train.shape[0]))
      print ("number of test examples = " + str(X_test.shape[0]))
      print ("X_train shape: " + str(X_train.shape))
      print ("Y_train shape: " + str(Y_train.shape))
      print ("X_test shape: " + str(X_test.shape))
      print ("Y_test shape: " + str(Y_test.shape))

    • 训练

      1
      model.fit(X_train, Y_train, epochs = 2, batch_size = 32)

  • 进行预测

    1
    2
    3
    preds = model.evaluate(X_test, Y_test)
    print ("Loss = " + str(preds[0]))
    print ("Test Accuracy = " + str(preds[1]))

测试自己的图片

1
2
3
4
5
6
7
8
9
10
img_path = 'images/my_image.jpg'
img = image.load_img(img_path, target_size=(64, 64))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
print('Input image shape:', x.shape)
my_image = scipy.misc.imread(img_path)
imshow(my_image)
print("class prediction vector [p(0), p(1), p(2), p(3), p(4), p(5)] = ")
print(model.predict(x))

对模型进行总览

  • 表格

    1
    model.summary()

  • 位图

    1
    2
    plot_model(model, to_file='model.png')
    SVG(model_to_dot(model).create(prog='dot', format='svg'))

结论

  • 实际中非常深的普通网络不起作用，因为梯度下降它们很难训练
  • 跳跃连接帮忙解决跳跃连接问题，它们也使得残差网络很容易学习 identity function
  • 有两种主要的组块：The identity block and the convolutional block
  • 把这些组块堆叠起来可以形成很深的残差网络
吴恩达深度学习笔记AIcnnKeras
微信捐赠
支付宝捐赠