cnn 辅助函数的构建
这周的编程作业内容是使用 numpy 实现卷积层和池化层,包括前向传播和方向传播。
包的引入
1 | import numpy as np |
作业大纲
- 卷积函数,包括:
- 零填充
- 卷积窗口
- 卷积前向传播
- 卷积反向传播
- 池化函数,包括:
- 池化前向传播
- 创造 mask
- Distribute value
- 池化反向传播
注意:每一步前向传播都需要储存一些参数在 cache 中,以便方向传播时可以用
卷积神经网络
先构建两个辅助函数。
零填充 Zero-Padding
该辅助函数的作用是在该图片周围加零,如下图所示:
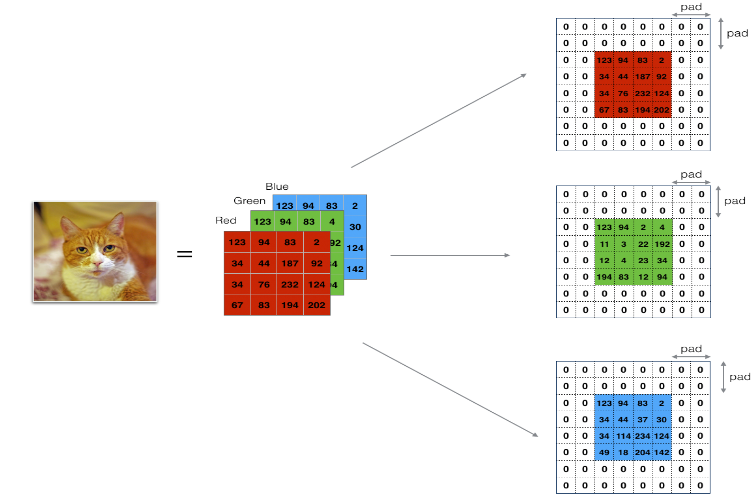
- 它使图片在通过卷积层时尺寸不会减小,对深层网络尤其有效
- 使我们保留边缘的重要信息
代码如下:
1 | def zero_pad(X, pad): |
单步卷积运算
- 取出输入向量
- 在输入的每个位置使用过滤器进行卷积
- 输出另一个向量
代码如下:
1 | def conv_single_step(a_slice_prev, W, b): |
卷积神经网络——前向传播
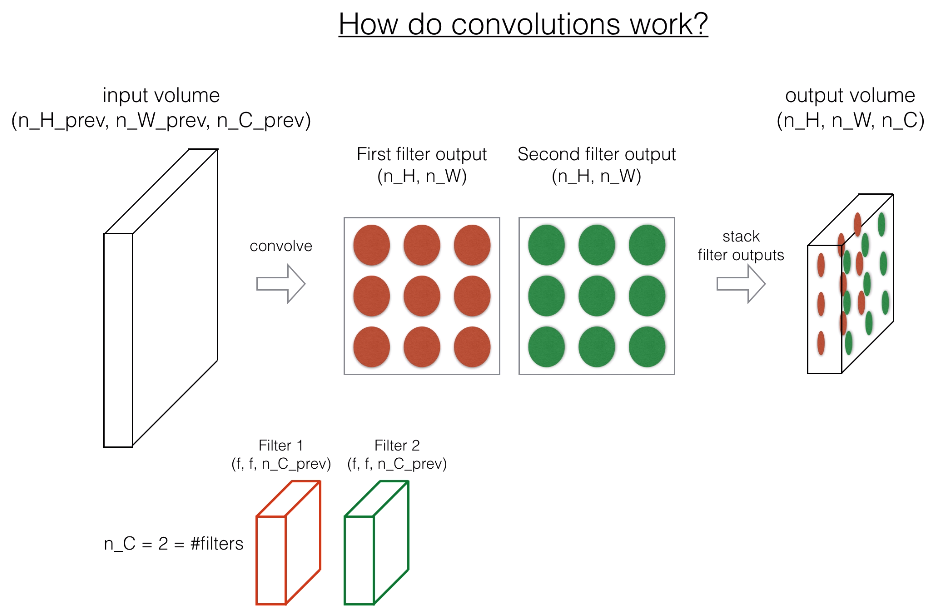
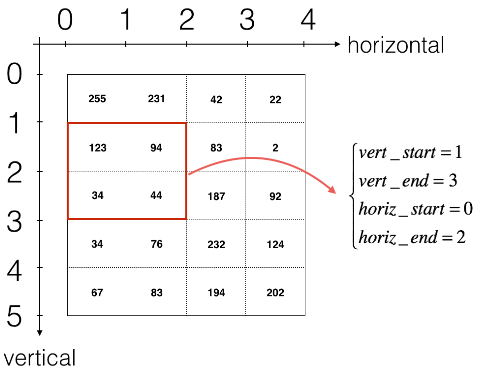
切片方法:
代码如下:
1 | def conv_forward(A_prev, W, b, hparameters): |
池化层
池化层减小了输入的高度和宽度,帮助减少计算量,使得特征检测器在输入中的位置更加不变。
- max pooling
- average pooling
池化层没有参数学习,只需要确定超参数,例如滤波器的大小。
代码如下:
1 | def pool_forward(A_prev, hparameters, mode = "max"): |
cnn 中的反向传播
卷积层
这部分是可选项,在课程中也没有给详细的推导过程和解释,具体的解释可以参考以下几个网站:
在参考 1 中我们可以知道,$dA^{[l-1]}$ 就是将 $dZ^{[l]}$ 与翻转 180 度的过滤器矩阵进行卷积的结果,如下图所示:
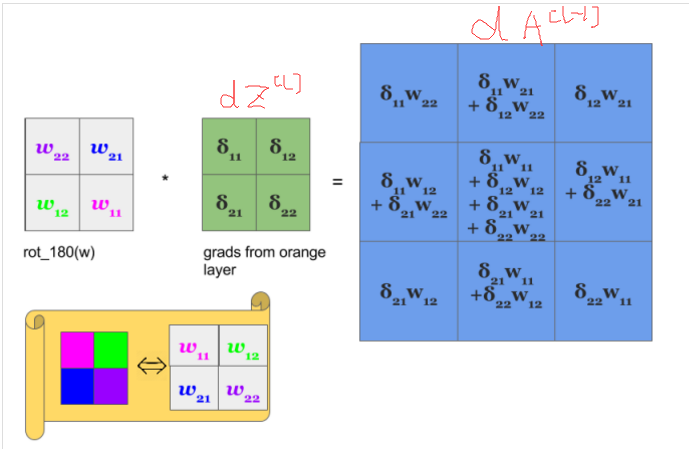
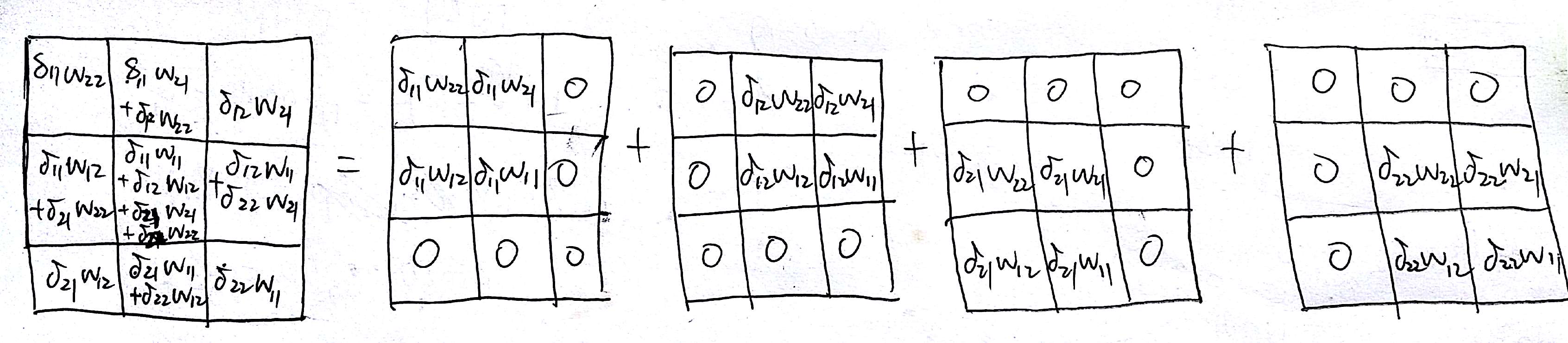
这正是下面式子所表示的,+= 就是将四个叠加起来,问题是下面的式子中的 W 并没有旋转 180 度……这点一直无法解释……
1 | da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c] |
1 | dW[:,:,:,c] += a_slice * dZ[i, h, w, c] |
1 | db[:,:,:,c] += dZ[i, h, w, c] |
1 | def conv_backward(dZ, cache): |
池化层
虽然池化层没有参数,但是还是需要将梯度反向传播到池化层的上一层,以便反向传播能继续下去。
max pooling
对于 max pooling 而言,只有原来的最大值才对最终的代价函数有影响,所以我们只需要计算代价函数对这个最大值的梯度即可,其他的置为零,首先创造一个蒙板函数:
1 | def create_mask_from_window(x): |
average pooling
由于 average pooling 中过滤器中每个值都对最终结果有影响,所以这每个值的梯度都是下一层梯度的平均一份,因为它们每个数对最终代价函数的贡献都是一样的,所以我们将一个梯度分散为若干个相等的梯度:
1 | def distribute_value(dz, shape): |
合并到一个函数
1 | def pool_backward(dA, cache, mode = "max"): |
cnn 的应用
这部分使用 tensorflow 来构建一个分类器。
包的引入和数据集
1 | import math |
1 | # 加载数据集 |
仍然是识别手势的数据集:
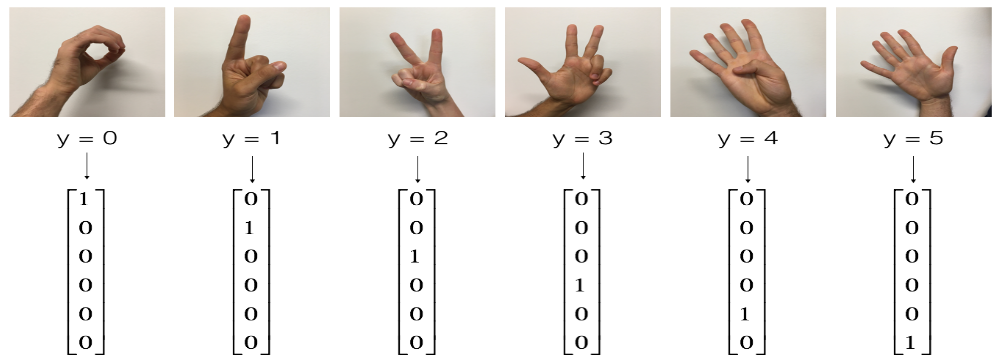
1 | # 图片示例 |
1 | # 数据集信息 |

创建占位符
首先需要创建输入数据的占位符,以便在运行 sess 时可以喂数据进去。
1 | # 创建占位符 |
初始化参数
- 初始化使用 W = tf.get_variable(“W”, [1,2,3,4], initializer = …)
- 初始化器使用 tf.contrib.layers.xavier_initializer(seed = 0)
1 | # 参数初始化 |
前向传播
卷积层 (步长 1,same 填充) -> RELU 激活 -> maxpool 池化(8×8过滤器,8×8步长,same 填充) -> 卷积层(步长 1,same 填充)-> RELU 激活 -> maxpool 池化(4×4 过滤器,4×4 步长)->拍扁 -> 全连接层(输出结点 6 个,不需要调用 softmax,因为在 tensorflow 中,softmax 和代价函数被整合进一个函数中)
使用的函数为:
- 卷积层:
tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = 'SAME')- X 为输入,W1 为过滤器,strides 必须为 [1,s,s,1],s 为步长,padding 类型为 same
- maxpool 池化层:
tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME')- f 为过滤器尺寸
- relu:
tf.nn.relu(Z1)- Z1 可以是任意形状
- 拍扁:
tf.contrib.layers.flatten(P)- 返回一个 [batch_size,k] 的张量,也就是说会保留样本个数那个维度
- 全连接层:
tf.contrib.layers.fully_connected(F, num_outputs)- num_outputs 为输出层结点个数
- 注意:tensorflow 会自动帮我们初始化全连接层的参数并在训练模型的时候自动训练,所以不用初始参数
1 | # 前向传播 |
计算代价函数
- 计算所有样例的损失函数:
tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y)- 返回所有样例的损失函数的一个向量
- 计算损失函数均值(代价函数):
tf.reduce_mean()
1 | # 计算代价函数 |
总模型
- 创造占位符
- 初始化参数(全连接层不要)
- 前向传播
- 计算损失
- 创建优化器
- 小批量梯度下降
1 | # 总模型 |
Tensorflow 使用感想
在 tensorflow 中,计算图中的任何值都不会被计算出来,除非你使用 sess.run(feed_dict)或者 tensor.eval(feed_dict),在求值的时候,从要求的值往前推,把这一条线上所有需要的 placeholder 找出来然后填入 feed_dict。


