错误分析
如果你想得到一个训练算法来做人类可以做的任务,但是训练的算法还没有达到人类的效果,你就需要手动地检查算法中的错误,来知道你下一步该做什么,这个过程叫做错误分析。
如何进行错误分析
假设训练一个分类猫的算法,准确率为 90%,错误率为 10%,我们对分错的样本进行检查,发现分错的样本中有一些把狗认成了猫,这时是否应该将重心转移到使分类器对狗的表现更好?
错误分析:
- 拿到约 100 张分类错误的开发集图片并进行手动检测
- 一般不需要检测上万张图片,几百张就足够了!
- 输出错误的图片里多少张狗
假设只有 5 张,那么在错误图片中只有 5% 的狗,如果在狗的问题上花了大量的时间,那么就算是最好的情况,也最多只是把错误率从 10% 降到 9.5%,所以并不值得。但是假设 100 张错误图片里有 50 张狗的图片,那么可以确定很值得将时间花在狗身上,因为错误率最多可能从 10% 降到 5%.
有时候我们可以并行考虑好几个 idea 是否值得付出努力。
假设有下面几个提高猫咪分类器性能的 idea:
- 提高对狗的识别
- 提高对其他猫科动物的识别
- 提高模型对模糊图像的性能
如何评估这几个方案,可以列一张表,记录每个分类错误的图片分属于哪一个错误类别,然后计算百分比:
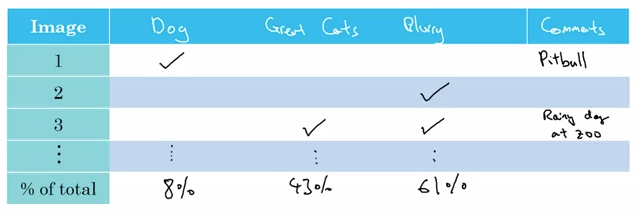
通过上面的分析我们可以知道现在应该专注于提高对模糊的图片(43%)或者猫科动物图片(61%)的准确度,但仅仅是一个参考,因为这取决于获得这些数据容不容易,假如要获得猫科动物的图片需要大量的时间,那么这一方面就可以先放放。
清除错误标记(标签)
当你检查数据集时发现一些输出标签 Y 标记错误,需不需要花时间修正这些标签。
对于训练集
- 深度学习算法在训练集上对于一些随机错误非常稳健,也就是说基本不需要管训练集上的一些随机的错误标记
- 但是注意算法对系统误差比较敏感,如果标记员一直把白色的狗标记为猫,那么训练出来的分类器也会学着这么做
对于开发/测试集
推荐的方法是在错误分析时增加一列“因为标签错误而分类错误”的统计:
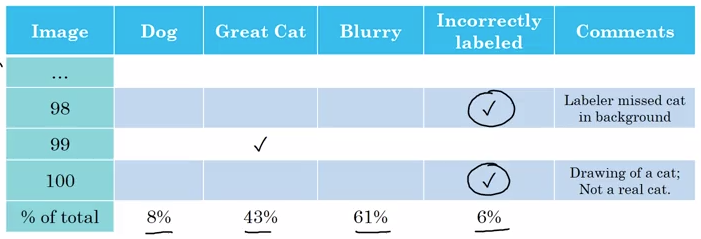
如上如图,加入标签错误是 6%,那么我们值得花时间去纠正这 6% 的样本的标签吗?
假设算法的总错误率是 10% 或 2%,考虑这两种情况下标签错误对评估的影响:
| 算法的总错误率 | 10% | 2% |
|---|---|---|
| 由标签错误引起的错误率 | 0.6% | 0.6% |
| 由其他因素引起的错误率 | 9.4% | 1.4% |
当总错误率为 10% 时,并不值得花时间去纠正这些错误的标签,因为即使纠正了也只提高 0.6% 的准确度,但是当总错误率为 2% 时,如果我们不纠正标签,那么他们引起的错误就占了一大半,这时纠正开发集中的标签错误就很有必要了。
纠正开发集/测试集的原则
- 对开发集和测试集进行一样的处理,确保他们来自相同的分布,当你纠正开发集中的一些问题,将这个过程也运用到测试集中
- 考虑检查你算法预测正确的和预测错误的样本
- 训练集 和 开发/测试集可以服从稍微不同的分布
建立第一个模型的建议
- 设立开发/测试集和评估指标
- 快速地建立一个不那么复杂的初始模型
- 使用偏差/方差分析/错误分析进行模型的迭代
训练集 和 开发/测试集 的不匹配
深度学习算法都希望有大量的训练数据,这导致很多团队将能找到的任何数据都塞进训练集,只为有更多的训练数据,即使很多这种数据来自于与开发集和测试集不同的分布。因此在深度学习时代,越来越多的团队正在使用的,训练数据并非来自与开发集和测试集相同的分布。
在不同的分布上进行训练和测试

要训练一个猫咪分类器,目前手上有两种数据,一种是从网上爬下来的十分精美的图片 200000 个,另一种是用户上传的质量很差的图片 10000 张,这两种数据的分布差异非常大,但是我们更关心的是右边用户上传的数据,是我们的“靶子”,现在有两种数据集分配方案。
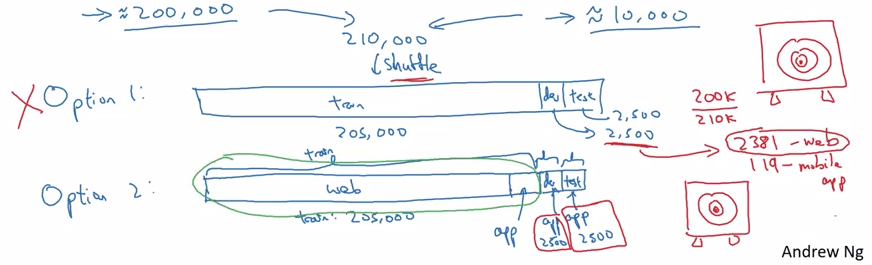
第一种是将所有图片混合洗牌,其中 205000 张作为训练集,剩下的 5000 张在开发/测试集之间平分。这种分法有一个很大的缺点!按照这种分法,开发集和测试集中按照比例可以算出用户上传的照片只有约 119 张,大部分都是网上爬的图片,并没有很好地反映我们所关心的数据(用户的图片),也就是说靶子放错了!
而正确的第二种分法是:将所有网上爬的 200000 张图片加上用户的 5000 张作为训练集,而剩下的用户的 5000 张平分为开发集和测试集,这样一来,你的开发集就瞄准了正确的目标。但缺点就是使得训练集分布和开发集分布有些不同,但是长期来说性能更好。
总结:
- 在某些情况下,可以允许训练集和开发/测试集来自不同的分布,以可以获得更大的训练集
- 但是注意:训练集中也需要包含足够的开发集分布数据,来避免数据不匹配问题!
数据分布不匹配时的偏差/方差分析方法
当你的训练集、开发集、测试集来自不同的分布时,偏差和方差的分析方法也会相应变化。
提出问题
对于一个猫分类器,假设人类误差是 0,且训练集和开发集数据来自不同分布,训练集误差为 1%,开发集误差为 10%,那么它们之间 9% 的差距到底是因为 (1)模型泛化能力不足导致方差太大,还是因为 (2)训练集数据分布不同?
解决办法
为了找出原因,我们定义一个新的数据集:训练-开发集 (training-dev set).
训练-开发集:将所有训练集数据洗牌,取出一小块作为训练-开发集,它的分布与训练集相同。
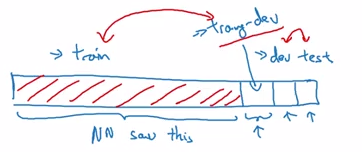
分布相同:
- 训练集 $\leftrightarrow$ 训练-开发集
- 开发集 $\leftrightarrow$ 测试集
划分好之后,计算出模型在如下各个数据集上的误差如下表:
| 例子 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 训练集误差 | 1% | 1% | 10% | 10% |
| 训练-开发集误差 | 9% | 1.5% | 11% | 11% |
| 开发集误差 | 10% | 10% | 12% | 20% |
- 例子1:训练集误差 1%,训练-开发集误差 9%,两者同分布都差距这么大,说明模型泛化能力不好,属于高方差问题。
- 例子2:在同样是在没训练过的数据集上预测,与训练集分布一样的训练-开发集误差很小,而与训练集分布不同的开发集(你所关心的)却误差很大,算法未在你所关心的分布上训练的很好,这就是数据不匹配问题 (mismatch problem)。
- 例子3:人类误差 0,训练集误差却高达 10%,这是明显是高偏差问题。
- 例子4:10% 说明高偏差;11%~20% 说明数据不匹配程度相当大。
train sets 和 dev/test sets 不匹配问题的通用的解决方案
一个模型可能的误差类型:
人类误差 (训练集分布) $<\overset{\text{反映了不同分布的识别难度大小}}{===========}>$ 人类误差 (开发集分布)
$\Updownarrow$ 反映可避免偏差
训练集误差 (训练集分布)
$\Updownarrow$ 反映方差情况
训练-开发集误差 (训练集分布)
$\Updownarrow$ 反映(训练集和开发集)数据不匹配情况
开发集误差 (开发/测试集分布)
$\Updownarrow$ 反映算法对开发集的过拟合情况,因为如果这个差距太大,则也许将神经网络
$\Updownarrow$ 调的太偏向开发集了,此时需要一个更大的开发集
测试集误差 (开发/测试集分布)
如何改善数据不匹配问题
- 人工分析误差,试着理解训练集与开发/测试集之间的差异
- 举个例子,在识别车载语音识别时,可能开发集中很多车辆噪音,而训练集没有,这是由实际情况决定的
- 想方设法使得训练集与之更相似:可以收集更多与开发/测试集相似的数据加入训练集,或者进行人工合成数据加入训练集,只要合成的数据让人类觉得很真实,那么就可以骗过算法
- 比如模拟车载噪音数据,将训练集中干净的音频加上一段噪音合成出噪音下的说话声。但是注意:一小段重复用来合成的汽车噪音会使得学习算法对这段声音产生过拟合
- 再比如无人驾驶中的汽车识别,可以通过三维建模画出我们需要的汽车样子。但是注意:建模所用的汽车模型非常有限,加入只有 20 种,那么神经网络很可能对这 20 种汽车产生过拟合
迁移学习 (Transfer learning)
什么叫迁移学习
深度学习中最有力的方法之一,是有时你可以把在一个任务中神经网络学习到的东西,应用到另一个任务中去。比如,你可以让神经网络学习去识别物体,比如猫,然后用学习到的(一部分)知识来帮助你更好地识别X射线的结果。这就是所谓的迁移学习。
如何实现
假如我们我们用猫狗的图片训练了一个如下的图片识别的神经网络:
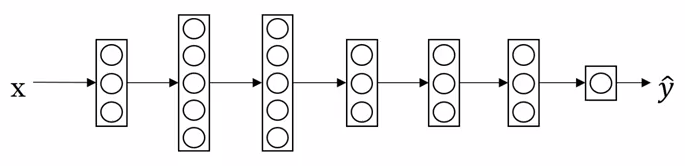
如果我们想把这个模型应用到另一个场景,比如 x 光片的诊断,实现方法是移除这个神经网络的最后一层和其相关的权重,如下图所示:
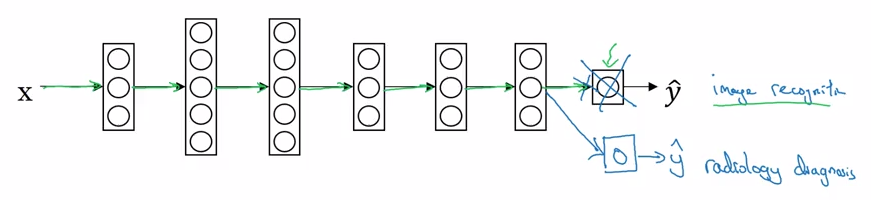
要实现迁移学习,要做的是:
- 将数据集换成 x 光诊断的图片
- 随机初始化新的最后一层的权重 W 和 偏差 b
- 重新训练该网络
- 如果数据量小:可以只训练最后一层的参数,保留其他的参数
- 如果数据量大:可以训练所有层
预训练 (pre training):我们把猫狗图片训练的模型用到其他地方,那么用猫狗图片对模型的训练就称之为预训练。预训练对模型的权重进行了预初始化,其他的训练是在预初始化权重的基础上继续训练。
微调 (fine tuning):在预训练的基础上继续训练,比如上面的再用 x 光诊断图片继续训练,对权重进行更新,称之为“微调”。
有时候你也可以将最后一层移除后增加一些新的层,然后对新建的几层重新训练:
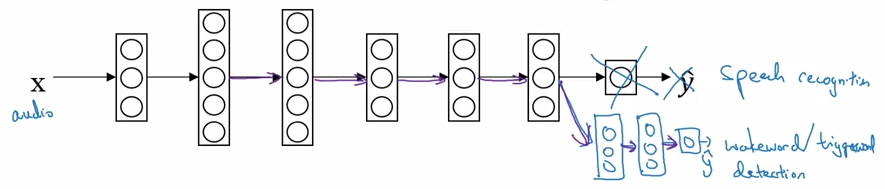
为什么迁移学习有效?
是因为从从大规模的图像识别数据集中学习到的边界检测,曲线检测,明暗对象检测等低层次的信息,或许能够帮助你的学习算法更好地去进行放射扫描结果的诊断。它会在图像的组织结构和自然特性中学习到很多信息,其中一些信息会非常的有帮助。所以当神经网络学会了图像识别意味着它可能学习到了以下信息:关于不同图片的点,线,曲面等等信息,在不同图片中看起来是什么样子的。或许关于一个物体对象的很小的细节,都能够帮助你在放射信息诊断的神经网络中,学习得更快一些或者减少学习需要的数据。
什么时候采用迁移学习?
任务 A 有着比任务 B 多得多的数据,可以从 A 迁移到 B
例如,假设你在一个图像识别任务中拥有一百万个样本,这就意味着大量数据中的低层次特征信息或者大量的有帮助的特征信息在神经网络的前几层被学习到了。但是对于放射扫描结果的诊断任务,或许仅仅是100个 X 光扫描样本。所以你从图像识别中学习到的大量的信息可以被用于迁移并且这些信息会有效地帮助你处理好放射诊疗。
总结:只能大数据模型迁移到小数据模型,而不能小数据模型迁移到大数据模型。
任务 A 和任务 B 有着相同的输入
- 例如识别猫狗和诊断 X 光输入的都是图片
当你认为任务 A 中的低层次特征会帮助到任务 B
- 例如你判断两个任务有某种可以互通的特征,比如两者都是识别物体或都是语音识别
多任务学习 (multi-task learning)
在多任务学习中,几个任务一起进行,让神经网络同时做几件事情。
如何实现
在自动驾驶时拍下一张照片需要识别出照片中是否存在一些物体,如果有就置 1,否则为 0 :

| 行人 | 0 |
|---|---|
| 汽车 | 1 |
| 交通牌 | 1 |
| 信号灯 | 0 |
于是输出标签变为(4,m)的矩阵:
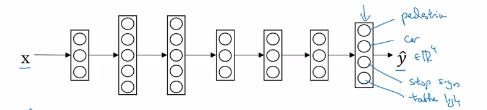
搭建上图中的网络进行训练,最后一层有四个单元,表示识别的四种物体的概率,那么代价函数可以表示为:
有时候 4 个标签会有缺失(下图中的 “?”),你仍然可以进行训练,只需要省略缺失项, $\sum\limits^{4}_{j=1}$ 只对有标签的值进行求和即可
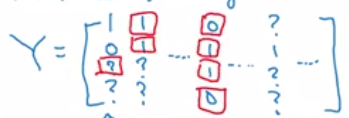
该方法相当于将四个独立的神经网络合在一起,但是效果更好
什么时候适用多任务学习
- 你要训练的任务共享一些低层次的特征
- 例如行人、交通灯、汽车、交通牌这些物体都是道路特征
- 非硬性:多任务中每个任务的数据量相当相似
- 如果你集中在某一任务上,其他任务比这单一任务有多得多的数据
- 如果你可以训练一个足够大的网络来做好所有的任务
- 如果神经网络不够大,与单独训练每个任务相比,多任务训练会损害准确率
端到端深度学习 (end-to-end deep learning)
什么是“端到端深度学习”
一个由许多阶段组成的学习系统,输入 x,输出 y,如果我们将其中的许多阶段用单个神经网络进行替代,直接建立从输入端 x 到输出端 y 的映射,就叫做“端到端深度学习”。
一些例子
例子 1
加入要建立一个语音识别系统,那么一般思路为:
输入音频 x $\xrightarrow{MFCC算法}$ 提取低级特征 $\xrightarrow{ML算法}$ 找到音素 $\xrightarrow{组合}$ 单词 $\xrightarrow{剪辑}$ 输出文字 y
而端到端深度学习的实现方式为直接建立输入语音 x 和文字脚本 y 的映射:
输入音频 x $\xrightarrow{ \quad \quad\quad\quad\quad\quad\quad 端到端深度学习 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}$ 输出文字 y
例子 2
机器翻译系统,传统机器学习思路:
英语 $\rightarrow$ 文本分析 $\rightarrow$ 提取特征 $\rightarrow$ … $\rightarrow$ 中文
端到端机器学习使用大量的英文和中文对应文本的数据集进行直接映射:
英文$\xrightarrow{ \quad \quad\quad\quad\quad 端到端深度学习 \quad\quad\quad}$ 中文
end-to-end DL 的优缺点
- 优点
- 端到端数据学习让数据“说话”,从 X $\rightarrow$ Y 的映射中更好地学习到数据内在的统计学特征,而不是被迫去反映人的先见
- 例如传统机器学习利用到语言中“音素”的概念,但是这个概念是是一个人造的产物,无法确定让算法使用“音素”是不是有利的
- 需要更少的人工设计组件,简化工作流程
- 端到端数据学习让数据“说话”,从 X $\rightarrow$ Y 的映射中更好地学习到数据内在的统计学特征,而不是被迫去反映人的先见
- 缺点
- 为了得到 X 到 Y 的映射,需要非常大量的 (X $\rightarrow$Y) 数据
- 它排除了一些具有潜在用途的手工设计组件
- 如果数据量不够,那么一个精心手工设计的系统实际上可以向算法中注入人类关于这个问题的知识,是很有帮助的
什么时候需要运用端到端深度学习
关键问题:你是否有充足的数据去学习出具有能够映射 X 到 Y 所需复杂度的方程?


