艺琛的 Livehouse主页学习笔记读书观影笔记个人随想爱好和生活相册所有博客特色标签关于我
coursera 吴恩达深度学习 Specialization 编程作业（course 2 week 2）
|学习笔记

本次作业实现了几种梯度下降算法，比较了它们的不同。

　普通梯度下降 (BGD)

所谓普通梯度下降就是一次处理所有的 m 个样本，也叫批量梯度下降 (Batch Gradient Descent)，公式为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def update_parameters_with_gd(parameters, grads, learning_rate):
    """
    普通梯度下降
    
    Arguments:
    parameters -- python dictionary containing your parameters to be updated:
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    grads -- python dictionary containing your gradients to update each parameters:
                    grads['dW' + str(l)] = dWl
                    grads['db' + str(l)] = dbl
    learning_rate -- the learning rate, scalar.
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
    """

    L = len(parameters) // 2	# 参数的个数

    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads['dW' + str(l+1)]
        parameters["b" + str(l+1)] =parameters["b" + str(l+1)] - learning_rate * grads['db' + str(l+1)]
        
    return parameters

随机梯度下降 Stochastic Gradient Descent (SGD)

SGD 一个只处理一个样本进行梯度下降，速度比 GD 快，但是在朝着最小值行进的过程中会发生震荡，而 GD 是平滑地稳步向最小值走。GD 是考虑周全再行动，每一步都朝着全局最优走，所以很慢，而 SGD 是走一步看一步，并不是每一步的迭代都朝着全局最优的方向走，噪声很多，如下图所示。

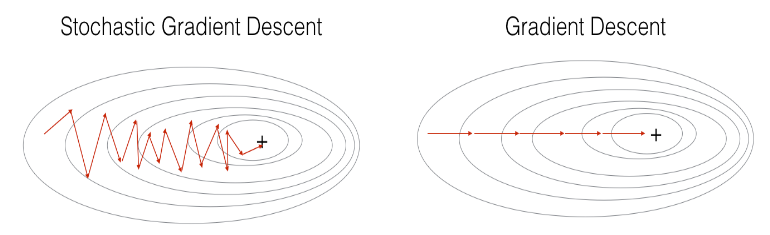
SGD 算法中有三个 for 循环：

  • 迭代次数的循环
  • 所有 m 个训练样例的循环
  • 神经网络所有层的循环
1
2
3
4
5
6
7
8
9
10
11
12
13
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
    for j in range(0, m):	# 遍历所有的 m 个训练样本
        # Forward propagation
        a, caches = forward_propagation(X[:,j], parameters)
        # Compute cost
        cost = compute_cost(a, Y[:,j])
        # Backward propagation
        grads = backward_propagation(a, caches, parameters)
        # Update parameters.
        parameters = update_parameters(parameters, grads)

小批量梯度下降 Mini-Batch Gradient descent (MBGD)

由于 BGD 和 SGD 是两个极端，如果一次既不处理一个样本，也不处理所有样本，而处理介于两者之间的样本数，即一次处理整个训练样本的一小批，学习速度会更快。

MBGD 比 SGD 的震荡更小：

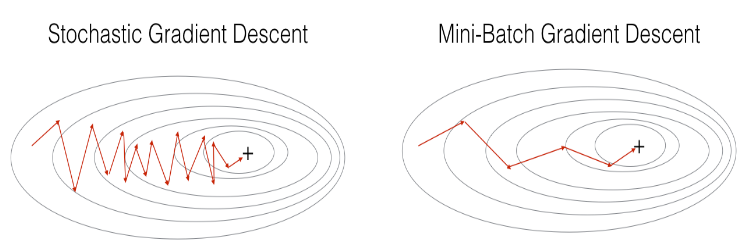
划分 mini -batch 的步骤

一共有两步：

  • 洗牌 (shuffle)：将训练集 （X，Y）进行随机的洗牌，打乱每一列的顺序，确保所有的样本会被随机分成不同的小批次。注意 X 和 Y 需要进行一样的洗牌操作，一一对应，如下图所示。

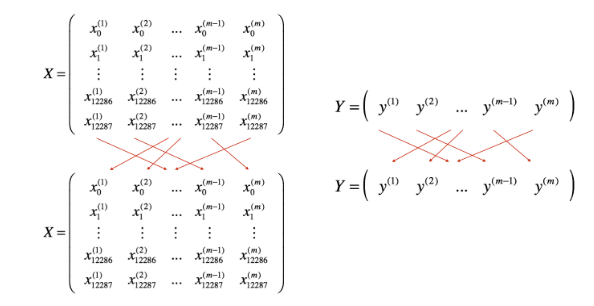
  • 划分 (Partition)：将训练集划分为每个大小为 mini_batch_size 的小批次。注意总样本数不一定总是能被 mini_batch_size 整除，所以最后一个小批次比 mini_batch_size 要小，如下图所示。

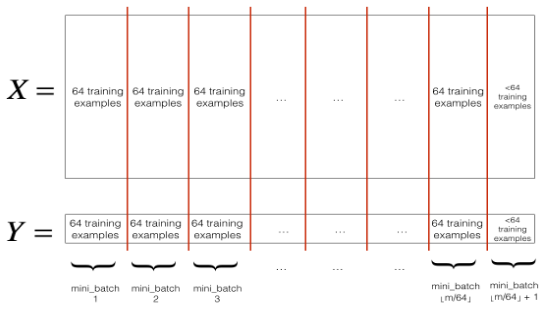
实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def random_mini_batches(X, Y, mini_batch_size = 64):
    """
    将总样本随机划分为许多小批次
    
    Arguments:
    X -- input data, of shape (input size, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
    mini_batch_size -- size of the mini-batches, integer
    
    Returns:
    mini_batches -- 存放划分好的(mini_batch_X, mini_batch_Y)的 list
    """
    
    m = X.shape[1]	# 总样本数
    mini_batches = []	# 存放划分好的最小批
        
    # 第一步：洗牌
    permutation = list(np.random.permutation(m))   # 生成 [0，1，2，...,m-1] 的数组并随机打乱
    shuffled_X = X[:, permutation]	# 将打乱的数组作为列标签，使得 X 的每列被随机打乱
    shuffled_Y = Y[:, permutation].reshape((1,m))	# 同上

    # 第二步：划分
    num_complete_minibatches = math.floor(m/mini_batch_size) # math.floor() 取整函数计算完整的 mini_batch 数目
    for k in range(0, num_complete_minibatches):	# 注意是从 0 开始，所以下面都是 k+1
        mini_batch_X = shuffled_X[:, k*mini_batch_size:(k+1)* mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k*mini_batch_size:(k+1)* mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)	# 组合成一个 tuple
        mini_batches.append(mini_batch)	# 将划分好的 tuple 放入 list 中
    
    # 单独处理最后一个数量小于 mini_batch_size 的批次
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches*mini_batch_size:]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches*mini_batch_size:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    return mini_batches

动量梯度下降

由于小批量梯度下降也会产生震荡问题，所以我们采用动量算法，考虑之前几次迭代的梯度来减小震荡。

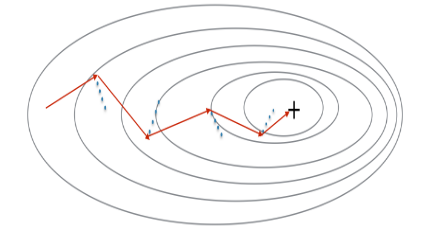
蓝色线是每一次梯度的方向，但是每次下降不沿着梯度方向走，而是沿着红线走，它是前几次梯度方向的加权平均值 v ——称之为“速度”。

初始化 v

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def initialize_velocity(parameters):
    """
    Initializes the velocity as a python dictionary with:
                - keys: "dW1", "db1", ..., "dWL", "dbL" 
                - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    
    Returns:
    v -- python dictionary containing the current velocity.
                    v['dW' + str(l)] = velocity of dWl
                    v['db' + str(l)] = velocity of dbl
    """
    
    L = len(parameters) // 2	# 神经网络层数
    v = {}
    
    for l in range(L):
        v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0],  parameters['W' + str(l+1)].shape[1] ))   # v_dW 和 dW 的维度相同
        v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0],  parameters['b' + str(l+1)].shape[1] ))   # v_db 和 db 的维度相同
        
    return v

更新参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    """
    用动量算法更新参数
    
    Arguments:
    parameters -- python dictionary containing your parameters:
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    grads -- python dictionary containing your gradients for each parameters:
                    grads['dW' + str(l)] = dWl
                    grads['db' + str(l)] = dbl
    v -- 初始化过的 v
    beta -- the momentum hyperparameter, scalar
    learning_rate -- the learning rate, scalar
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
    v -- python dictionary containing your updated velocities
    """

    L = len(parameters) // 2 # 神经网络层数

    for l in range(L):

        # 计算 v
        v["dW" + str(l+1)] = beta * v["dW" + str(l+1)] + (1 - beta) * grads["dW" + str(l+1)]
        v["db" + str(l+1)] = beta * v["db" + str(l+1)] + (1 - beta) * grads["db" + str(l+1)]
        # 更新参数
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]

    return parameters, v

Adam 算法

Adam 是训练神经网络最有效的算法之一，结合了动量算法和 RMSprop 算法的优点。

一共三步：

  • 计算之前梯度的指数加权平均 v，然后其计算偏差修正值 v_correct
  • 计算之前梯度的平方的指数加权平均 s，然后计算其偏差修正值 s_correct
  • 用上面的值更新参数

公式：

初始化 v 和 s

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def initialize_adam(parameters) :
    """
   初始化 v 和 s，他们的维度都和对应的梯度相同
    
    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters["W" + str(l)] = Wl
                    parameters["b" + str(l)] = bl
    
    Returns: 
    v -- python dictionary that will contain the exponentially weighted average of the gradient.
                    v["dW" + str(l)] = ...
                    v["db" + str(l)] = ...
    s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                    s["dW" + str(l)] = ...
                    s["db" + str(l)] = ...

    """
    
    L = len(parameters) // 2 
    v = {}
    s = {}
    
    for l in range(L):
        v["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0],  parameters['W' + str(l+1)].shape[1] ))
        v["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0],  parameters['b' + str(l+1)].shape[1] ))
        s["dW" + str(l+1)] = np.zeros((parameters['W' + str(l+1)].shape[0],  parameters['W' + str(l+1)].shape[1] ))
        s["db" + str(l+1)] = np.zeros((parameters['b' + str(l+1)].shape[0],  parameters['b' + str(l+1)].shape[1] ))
    
    return v, s

用 v 和 s 更新参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8):
    """
    用 Adam 算法更新参数
    
    Arguments:
    parameters -- 包含所有参数的字典
    grads -- 包含所有参数梯度的字典
    v -- 初始化过的 v
    s -- 初始化过的 s
    t -- 当前的批次
    learning_rate -- 学习率
    beta1 -- Exponential decay hyperparameter for the first moment estimates 
    beta2 -- Exponential decay hyperparameter for the second moment estimates 
    epsilon -- 防止分母为零的超参数

    Returns:
    parameters -- python dictionary containing your updated parameters 
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    """
    
    L = len(parameters) // 2	# 参数个数              
    v_corrected = {}	# 用来存放 v_correct
    s_corrected = {}	# 用来存放 s_correct
    
    # 实现 Adam 算法
    for l in range(L):
        # 计算 v 值
        v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1 - beta1) * grads["dW" + str(l+1)]
        v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1 - beta1) * grads["db" + str(l+1)]
        
        # 计算偏差修正过的 v 值
        v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - beta1 ** t)	# beta ** t 表示 beta 的 t 次幂 
        v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - beta1 ** t)
       
        # 计算 s 值
        s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1 - beta2) * np.square(grads["dW" + str(l+1)])	# np.square() 表示逐元素平方
        s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1 - beta2) * np.square(grads["db" + str(l+1)])
        
        # 计算偏差修正过的 s 值
        s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1 - beta2 ** t)
        s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1 - beta2 ** t)
       
        # 更新参数
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * ( v_corrected["dW" + str(l+1)] / (np.sqrt(s_corrected["dW" + str(l+1)]) + epsilon))	# np.sqrt() 为逐元素开平方
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * ( v_corrected["db" + str(l+1)] / (np.sqrt(s_corrected["db" + str(l+1)]) + epsilon))

    return parameters, v, s

比较几种优化算法的区别

  • 使用普通的批量梯度下降，调用函数：
    • update_parameters_with_gd()
  • 使用动量算法梯度下降，调用函数：
    • initialize_velocity() 和 update_parameters_with_momentum()
  • 使用 Adam 梯度下降，调用函数：
    • initialize_adam() 和 update_parameters_with_adam()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
    """
    可以使用不同优化函数的 3 层神经网络
    
    Arguments:
    X -- input data, of shape (2, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
    layers_dims -- python list, containing the size of each layer
    learning_rate -- the learning rate, scalar.
    mini_batch_size -- the size of a mini batch
    beta -- Momentum hyperparameter
    beta1 -- Exponential decay hyperparameter for the past gradients estimates 
    beta2 -- Exponential decay hyperparameter for the past squared gradients estimates 
    epsilon -- hyperparameter preventing division by zero in Adam updates
    num_epochs -- number of epochs
    print_cost -- True to print the cost every 1000 epochs

    Returns:
    parameters -- python dictionary containing your updated parameters 
    """

    L = len(layers_dims)             
    costs = []                       
    t = 0                           
    
    # 初始化参数
    parameters = initialize_parameters(layers_dims)

    # 初始化优化函数
    if optimizer == "gd":
        pass # 普通梯度下降没有初始化要求
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)	# 初始化动量算法
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)	# 初始化 Adam 算法
    
    # 优化算法循环
    for i in range(num_epochs):
        
        minibatches = random_mini_batches(X, Y, mini_batch_size)	# 划分最小批

        # 不同批次的循环
        for minibatch in minibatches:

            # 从 minibatchs 中取出当前最小批
            (minibatch_X, minibatch_Y) = minibatch

            # 前向传播
            a3, caches = forward_propagation(minibatch_X, parameters)

            # 计算代价函数
            cost = compute_cost(a3, minibatch_Y)

            # 反向传播
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)

            # 更新参数，三种方式
            if optimizer == "gd":	
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)	# 批量（普通）梯度下降更新参数
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)	# 动量梯度下降更新参数
            elif optimizer == "adam":
                t = t + 1 # 当前的批次，Adam 算法与 t 有关
                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t, learning_rate, beta1, beta2, epsilon)
        
        # 每一千步打印一次代价函数
        if print_cost and i % 1000 == 0:
            print ("Cost after epoch %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
                
    # 代价函数画图
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters

使用 MBGD

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

结果如下：

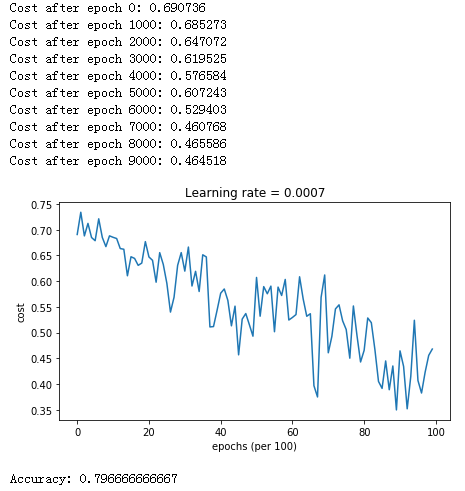
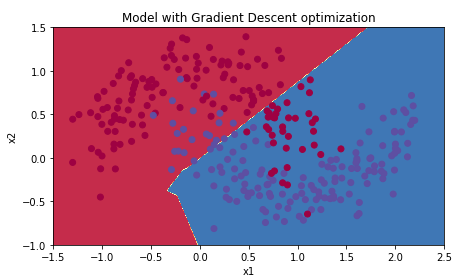
使用动量算法

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

结果：

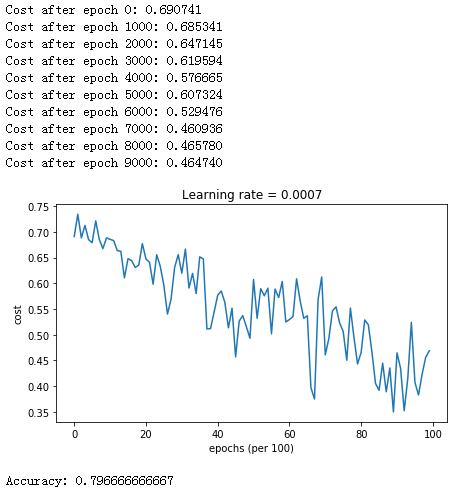
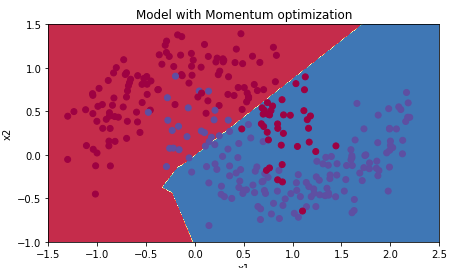
使用 Adam 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

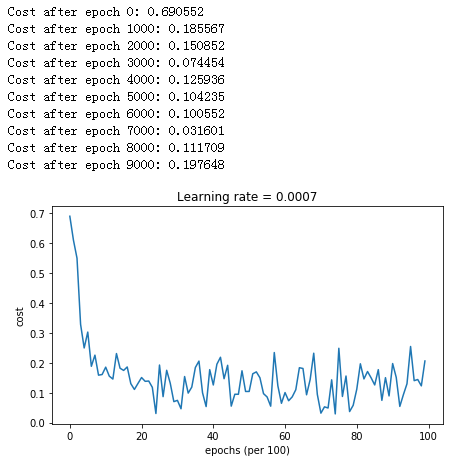
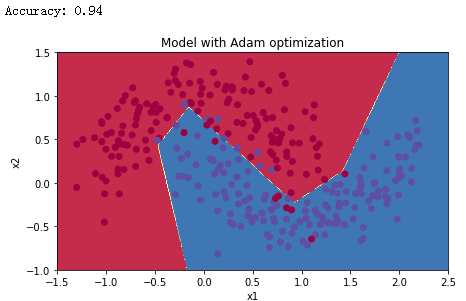
总结

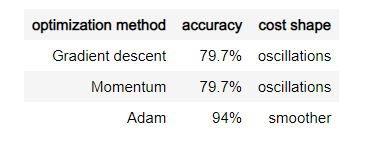
  • 动量算法经常会有帮助，但是在小学习率和简单的的数据集中它的影响几乎可以忽略。
  • 代价函数的震荡是因为某些小批次的数据噪声更多
  • Adam 算法比动量算法和 MBGD 表现精确度更高，但是如果给足够的时间，三个算法都会得到很好的精确度，但是这说明 Adam 算法运行更快
  • Adam 算法的优点
    • 虽然比动量算法和 MBGD 所需的内存更多，但是相对来说所需内存还是较少
    • 几乎不需要怎么调整它的超参数 $\beta_1,\beta_2,\varepsilon$ ，直接使用默认值，就能得到很好的结果
吴恩达深度学习笔记AI优化算法梯度下降
微信捐赠
支付宝捐赠