本周主要学习不同的参数优化方式，提高模型的训练速度。

小批量梯度下降算法 (mini-batch gradient descent)

算法介绍

向量化可以有效率地同时计算 m 个样本，但是当样本数为几百万时，速度依然会很慢，每一次迭代都必须先处理几百万的数据集才能往前一步，所以我们可以使用这个算法进行加速。

首先我们将训练集划分为一个一个微小的训练集，也就是小批量训练集 (mini-batch)，比如每一个微小训练集只有 1000 个样本：

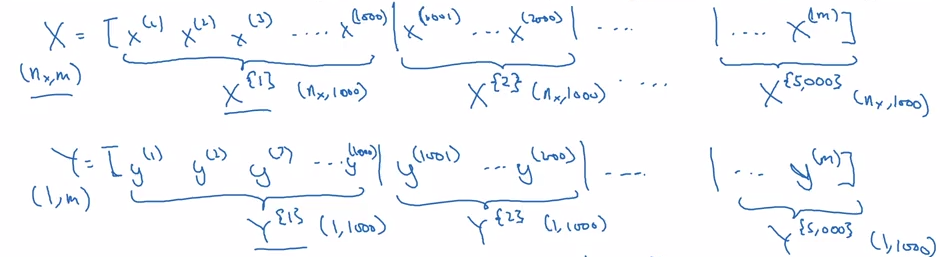
我们把第 t 个批次的数据用上标 {t} 表示，例如 $X^{\{t\}},Y^{\{t\}}$

$for \quad t = 1,…,5000: (每一步用 (X^{\{t\}},Y^{\{t\}}) 做一次梯度下降)\\ \quad X^{\{t\}} 为输入的前向传播 (1000 个样例)\\ \quad 计算代价函数 J^{\{t\}}\\ \quad 反向传播计算梯度 (只用 X^{\{t\}} 和 Y^{\{t\}})\\ \quad 更新参数 $

以上是对训练集的一次迭代，可以得到 5000 次梯度逼近，继续使用另一个 for 循环进行多次迭代。

理解算法

小批量梯度下降 (mini-batch gradient descent) 和批量梯度下降 (batch gradient descent) 中代价函数的变化如下图：

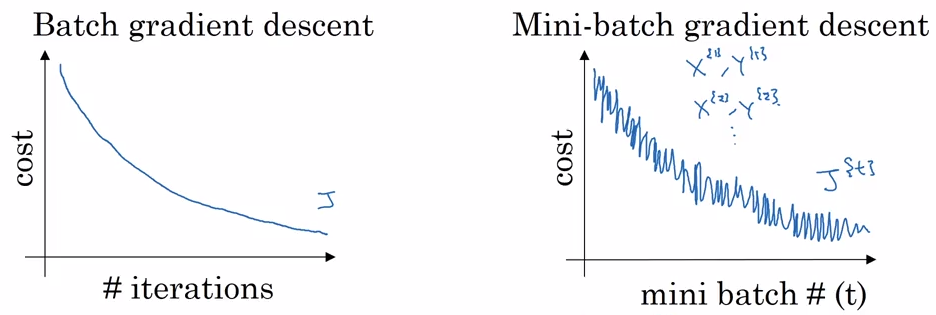
梯度下降有三种类型，根据每个批次的样本数不同划分：

• 若 minibatch 尺寸 = m，称之为：批量梯度下降 (BGD) ( X{t} , Y{t} ) = ( X , Y )
• 若 minibatch 尺寸 = 1，称之为：随机梯度下降 (SGD) ( X{t}, Y{t} ) = ( X{1}, Y{1} ), ( X{2}, Y{2} ) ,…, ( X{m}, Y{m} )
• 若 minibatch 尺寸介于 1 到 m 之间：小批量梯度下降 (MBGD)

在实际中一般采用第三种，因为第一种和第二种都有缺点：

• 随机梯度下降失去了使用向量加速的机会，而且会发生震荡，但是速度比批量梯度下降快
• 批量梯度下降的缺点是如果训练集太大，在每次的迭代上要花费太长的时间
• 小批量梯度下降，则既可以利用到向量化，又可以不用等待整个训练集都遍历一遍就可以进行梯度下降，而且震荡要比随机梯度下降要小，是最好的方案

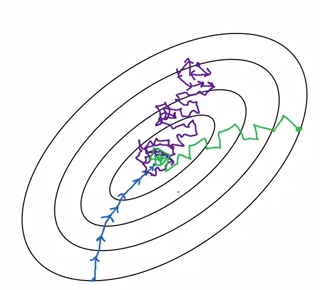
下图展示了不同梯度下降的过程，蓝线是批量梯度下降，绿线是小批量梯度下降，紫线是随机梯度下降。

如何选择 mini-batch 的 size

最小批包含的样本数是一个可调的超参数，用如下原则来确定：

• 如果训练集很小（m < 2000）：直接使用批量梯度下降
• 如果训练集很大：一般选择 64 ～ 512 作为每个批次的大小，由于计算机内存的布局和访问方式，把它设为 2 的幂数代码运行会更快，故一般选择 64，126，256，512 这几个值
• 确保 minibatch 的 X{t} 和 Y{t} 能够放进 CPU 和 GPU 的内存

指数加权平均 (Exponentially weighted averages)

什么是指数加权平均

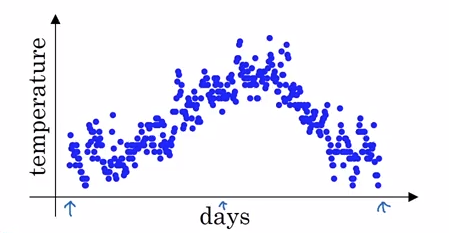
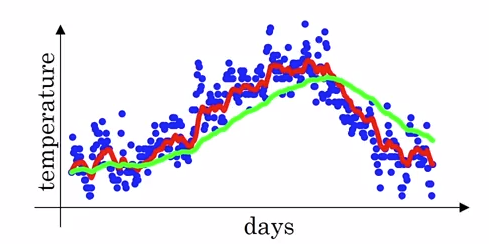
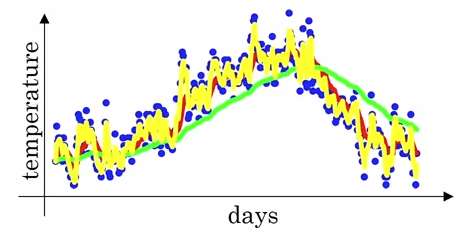
上图表示的是伦敦一年 365 天气温的散点图，第 t 天的气温值为 $\theta_t$，给出如下公式计算指数加权平均 (统计学中称为“指数加权滑动平均”)：

$$v_t=\beta v_{t-1}+(1-\beta)\theta_t$$

其中 $v_t$ 可以近似认为是前 $\frac{1}{1-\beta}$ 天的气温平均值，例如：

• 若 $\beta = 0.9$ 则 $v_t$ 可认为计算的是前 10 天的平均气温值，如红线所示
• 若 $\beta = 0.98$ 则 $v_t$ 可认为计算的是前 50 天的平均气温值，如绿线所示
• 若 $\beta = 0.5$ 则 $v_t$ 可认为计算的是前 2 天的平均气温值，如黄线所示

理解指数加权平均

如何实现

$$v_0=0\\v_1=\beta v_0+(1-\beta)\theta_1\\v_2=\beta v_1+(1-\beta)\theta_2\\v_3=\beta v_2+(1-\beta)\theta_3\\...$$

伪代码：

$v_\theta=0\\repeat\{\\ \quad \quad \quad get \ next \ \theta_t \\ \quad \quad \quad v_\theta:=\beta v_\theta+(1-\beta)\theta_t\\ \quad \quad \quad \}$

小技巧：偏差修正

当 $\beta=0.98$ 时，我们预计会得到绿色那条线：

但是实际上我们会得到下图紫色那条线：

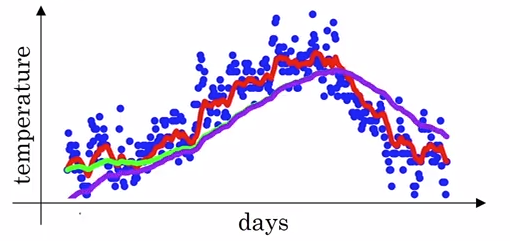
根据公式 $v_t=\beta v_{t-1}+(1-\beta)\theta_t$ ：
$v_0=0\\v1=0.98v_0+0.02\theta_1=0.02\theta_1\\v_2=0.98v_1+0.02\theta_2=0.98*0.02\theta_1+0.02\theta_2$

可以看到 $v_2$ 的值将远小于 $\theta_1$ 和 $\theta_2$ ，造成估计的偏差，有一种方法可以在估算的初期将偏差修正：

$$v_t=\frac{v_t}{1-\beta^t}$$

$t=2:1-\beta ^t=1-0.98^2=0.0396\\\frac{v_2}{0.0396}=\frac{0.0196 \theta_1 + 0.02\theta_2}{0.0396} \rightarrow \theta_1 和 \theta_2的加权平均数，从而消除了偏差$

当 $t​$ 逐渐增大，$\beta^t​$ 的值将趋于 0，修正偏差基本无影响，所以绿线和紫线在后半段几乎重合。

动量梯度下降算法 (Gradient descent with momentum)

普通梯度下降的困境

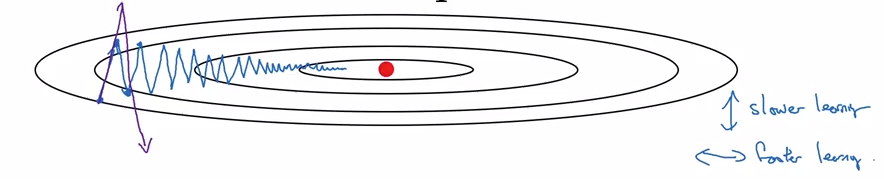
• 红点是梯度下降最小点，对于普通的梯度下降，路径如蓝线所示，朝着最小值缓慢地震荡前进，这种震荡会减慢学习的速度
• 不能使用太大的学习率，否则会产生超调，产生发散，无法收敛到最小点
• 在上下方向希望学习慢一点，因为不希望出现那些震荡，水平方向希望学习快一点，因为希望快速从左到右

动量梯度下降步骤

$v_{dW}=0(维度和dW相同)\\v_{db}=0(维度和db相同)\\在第 t 次迭代：\\ \quad \quad 计算当前小批次的 dW，db \\ \quad \quad v_{dW}=\beta v_{dW}+(1-\beta)dW \\ \quad \quad v_{db}=\beta v_{db}+(1-\beta)db \\ \quad \quad W:=W-\alpha v_{dW},b:=b-\alpha v_{db} $

• 超参数 $\alpha, \beta$ ， 其中 $\beta = 0.9$ 效果最好，相当于计算前十次迭代的梯度平均值
• 一般不需要对 $v_{dW},v_{db}$ 进行偏差修正
• 另一个版本为 $v_{dW}=\beta v_{dW}+dW,v_{db}=\beta v_{db}+db$ 也是正确的，但吴恩达不推荐

算法解释

解释：这些操作可以让梯度下降变得平滑，因为 $v_{dW}$ 计算的是这一次迭代之前的若干次的梯度的平均值，震荡的路径在纵轴方向是 $\nearrow \searrow \nearrow \searrow$ ，这些梯度一正一负，相互抵消，在纵轴方向的平均值趋于 0 ，减弱了震荡，而横轴方向是 $\rightarrow \rightarrow\rightarrow\rightarrow$ ，都指向了右边，所以横轴方向的平均值依然很大。

形象解释：把代价函数图像想象成一个碗，有一个球滑向碗的最低点，把导数项 dW 和 db 想象成球滚下时的加速度，而把动量项 $v_{dW},v_{db}$ 想象成球的速度。

导数项给了球一个加速度，然后球向下滚，因为有加速度，所以它滚得越来越快，因为$\beta$ 是一个略小于1的数，可以把它看作摩擦力，让球不至于无限加速下去。与梯度下降中每一步都独立于之前步骤所不同的是，现在你的球可以向下滚并获得动量，沿碗向下加速并获得动量。

均方根传递梯度下降算法——RMSprop 算法 (Root Mean Square prop)

仍然是这个震荡的问题，为了便于理解，假设只有两个参数 w 和 b，我们可以看到要减小震荡，必须使得纵轴即参数 b 的学习速度很慢，而横轴即参数 w 的学习速度很快，我们仍然使用指数加权平均的知识来实现梯度下降。

RMSprop 实现步骤

$ S_{dW}=0(维度和dW相同)\\S_{db}=0(维度和db相同)\\在第 t 次迭代：\\ \quad \quad 计算当前小批次的 dW，db \\ \quad \quad S_{dW}=\beta’ S_{dW}+(1-\beta’)(dW)^2 \\ \quad \quad S_{db}=\beta’ S_{db}+(1-\beta’)(db)^2 \\ \quad \quad W:=W-\alpha \frac{dW}{\sqrt{S_{dW}}+\varepsilon },b:=b-\alpha \frac{db}{\sqrt{S_{db}}+\varepsilon } $

• $\beta’$ 是为了和动量算法中的 $\beta$ 相区分
• $(dW)^2$ 是逐元素平方
• $\varepsilon$ 是一个非常小的数比如 $10^{-8}$ 确保分母不为零

算法理解

如上图所示，我们希望纵轴参数 b 的梯度很小，学习更慢，减小震荡，希望横轴参数 w 的梯度很大，学习更快，也就是希望作为分母的 $\sqrt{S_{dW}}$ 很小，而 $\sqrt{S_{db}}$ 很大。由于纵轴方向上是震荡的，路径更加偏向 b 轴一些，所以 $(db)^2$ 会相对更大，从而$\sqrt{S_{db}}$ 会相对更大，而 $(dW)^2$ 会相对更小，从而 $\sqrt{S_{dW}}$ 相对更小。

自适应矩估计梯度下降算法——Adam 算法 (Adaptive Moment Estimation)

这是一种结合了动量算法和 RMSprop 两者优点的算法，被广泛使用且已经被证明在很多不同种类的神经网络架构中都十分有效。

Adam 实现步骤

$v_{dW}=0,S_{dW}=0,v_{db}=0,S_{db}=0 \leftarrow 初始化\\ 在第 t 次迭代：\\ \quad 计算当前小批次的 dW，db \\ \quad v_{dW}=\beta_1 v_{dW}+(1-\beta_1)dW ，v_{db}=\beta_1 v_{db}+(1-\beta_1)db \leftarrow 动量算法\\ \quad S_{dW}=\beta_2 S_{dW}+(1-\beta_2)(dW)^2，S_{db}=\beta_2 S_{db}+(1-\beta_2)(db)^2 \leftarrow RMSprop\\ \quad v_{dW}^{correct}=\frac{v_{dW}}{1-\beta_1^t}，v_{db}^{correct}=\frac{v_{db}}{1-\beta_1^t} \leftarrow v 的偏差修正 \\ \quad S_{dW}^{correct}=\frac{S_{dW}}{1-\beta_2^t}，S_{db}^{correct}=\frac{v_{db}}{1-\beta_2^t} \leftarrow S 的偏差修正 \\ \quad W:=W-\alpha \frac{v_{dW}^{correct}}{\sqrt{S_{dW}^{correct}}+\varepsilon },b:=b-\alpha \frac{v_{db}^{correct}}{\sqrt{S_{db}^{correct}}+\varepsilon } \leftarrow 更新参数$

超参数的默认值

• 学习率 $\alpha$ ：尝试不同值比较效果
• $\beta_1：0.9$
• $\beta_2:0.999$
• $\varepsilon:10^{-8}$

参数为 $\beta_1$ 的梯度值的指数加权平均 $v$ 称为第一阶的矩，参数为 $\beta_2$ 的梯度平方值的指数加权平均 $S$ 被称为第二阶的矩

学习率衰减 (learning rate decay)

为什么需要学习率衰减

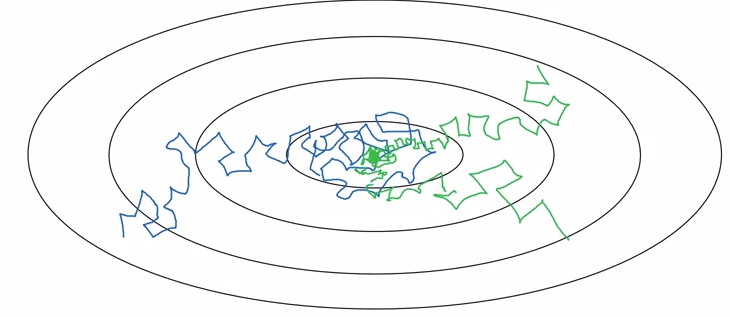
假如我们采用固定步长，如蓝色路径所示，那么它会逐步向最小值靠近，但不会完全收敛到这点，所以算法会在最小值周围浮动，但是却永远不会真正收敛。

如果慢慢地衰减学习率，刚开始学习率取值较大，学习速度较快，但随着学习率的的逐渐衰减，步长也会逐渐减小，所以最后将围绕着离极值点更近的的区域摆动，不会继续漂流远离。

如何实现

1 次迭代（1 epoch）：遍历完一次数据集，完成一次梯度更新

学习率衰减就是使学习率随着迭代次数 epoch _num 单调递减，比如下面这个公式：

$$\alpha = \frac{1}{1+decay\_rate*epoch\_num}\alpha_0$$

• decay_rate 为衰减率，是一个超参数
• epoch_num 是迭代次数
• $\alpha_0$ 是初始学习率，也是一个超参数

代一些具体值看看学习率衰减的情况：

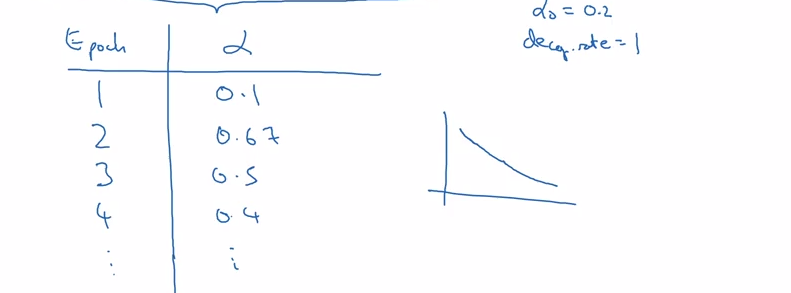
还有一些其他的学习率衰减公式，比如下面这个：

$$\alpha = 0.95 ^{epoch\_num}\alpha_0$$

• 使得学习率呈指数级下降

还有：

$$\alpha = \frac{k}{\sqrt{epoch\_num}}\alpha_0 \ \ 或者\frac{k}{\sqrt{t}}\alpha_0$$

还有采用离散阶梯函数的学习率衰减，比如下图所示：

有时候人们还会使用手动的梯度衰减，但是比较少。

局部最优问题 (the problem of local optima)

深度学习早期，人们担心优化算法会陷入局部最优之中。

什么是局部最优

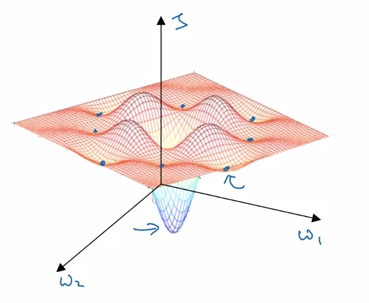
假设上图中是参数 w1 和 w2关于代价函数的三维图像，人们担心在对这些参数进行优化的时候会优化到图中蓝点所在的位置，这些值只是在“谷底”，而不是真正的最小值，是局部最优。

为什么不用担心局部最优问题

在训练一个神经网络时，代价函数中大部分梯度为零的点并不是上图中的局部最优，而是鞍点 (saddle point)，这种点周围的函数从一个方向看是凸函数，从另一个是凹函数，就像马鞍一样，如下图所示。

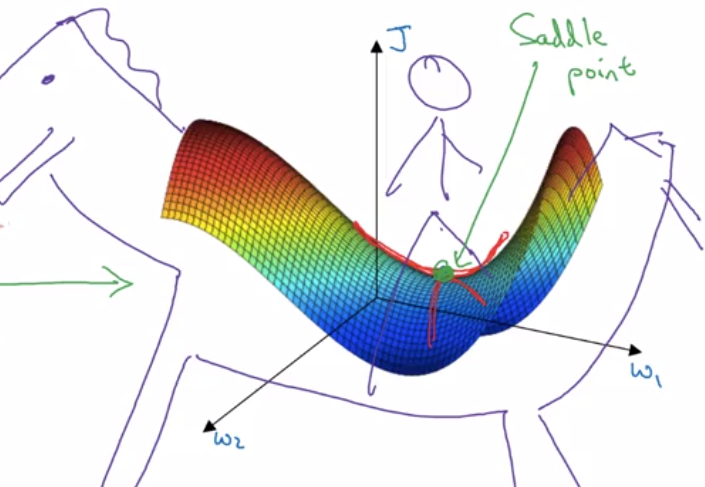
如果一个点要是局部最优点，那么这个点周围的函数需要在所有方向看都是凸函数或者都是凹函数，但是由于神经网络的参数有上万乃至上百万个，如果某个点要成为局部最优，那么在所有的上百万个维度中函数的方向都得是一样的凹函数或者凸函数，这件事发生的概率非常非常低。更有可能碰到的是鞍点，某些方向的曲线向上弯曲，某些方向的向下弯曲，并非所有的曲线都向上或者向下弯曲，所以在高维空间中，不用担心发生局部最优问题！

停滞区问题 (Plateaus)

停滞区：导数长时间接近于零的一段区域

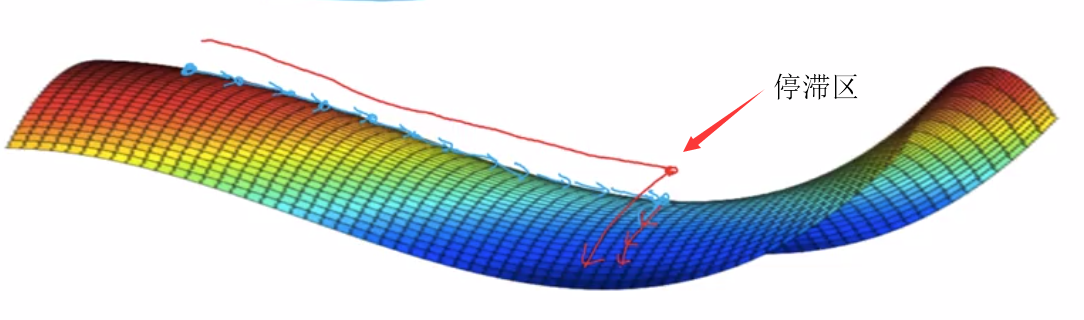
当沿着马鞍面向下移动，移动到鞍点，但鞍点不是我们需要的最小值点，需要继续往下移动。但是这个地方梯度为零或者接近于零，曲面很平，需要花费很长时间缓慢地在这个停滞区内找到这个点而不能继续往下，当左侧或右侧有随机扰动，才能继续往下走，这会让学习速度变得非常慢。

解决办法：采用 动量算法、RMSprop算法、Adam算法等可以改善这个情况。