艺琛的 Livehouse主页学习笔记读书观影笔记个人随想爱好和生活相册所有博客特色标签关于我
coursera 吴恩达深度学习 Specialization 编程作业（course 1 week 4）
|学习笔记

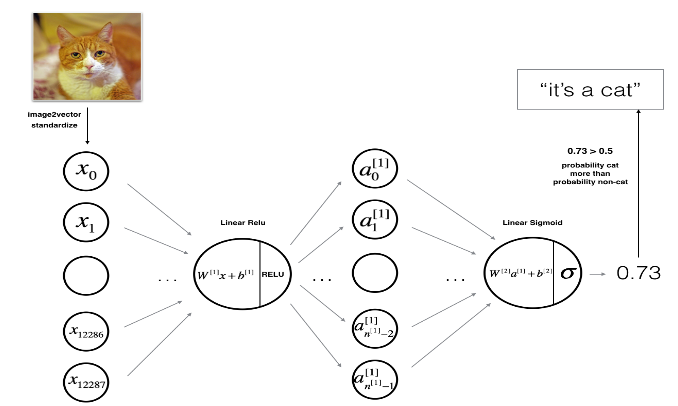
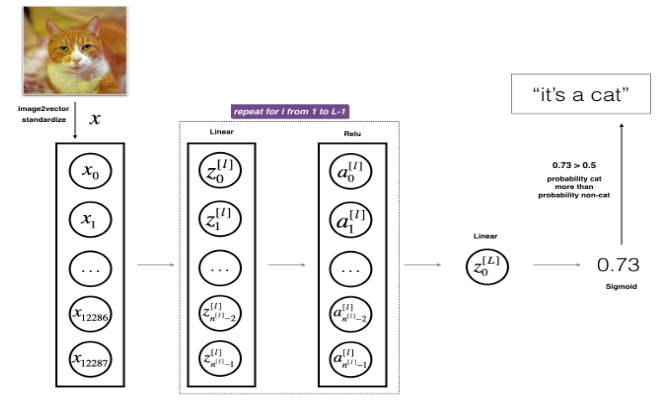
第一部分：基本架构

这是深度学习专项课程第一课第四周的编程作业的第一部分，通过这一部分，可以学到：

  • 使用非线性单元比如 ReLU 来提高模型
  • 建立一个更深的神经网络（大于一个隐藏层）
  • 实现一个易用的神经网络类

包的引入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 包的引入
import numpy as np
import h5py 
import matplotlib.pyplot as plt
from testCases_v4 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward

%matplotlib inline # %符号为ipython的魔法函数，与画图有关，在pycharm中会报错
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

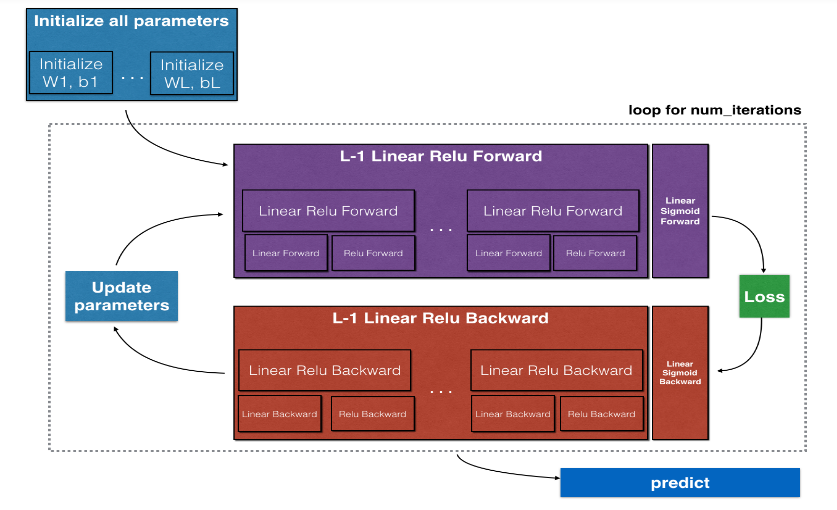
总体框架

  • 初始化一个两层神经网络的参数以及一个 L 层的神经网络的参数

  • 实现前向传播模块（下图中的紫色模块）

    • 实现某一层的前向传播步骤的线性部分（得到 $Z^{[l]}$）
    • 给定激活函数（relu/sigmoid）
    • 组合之前的两步形成一个[线性—>激活]前向传播函数
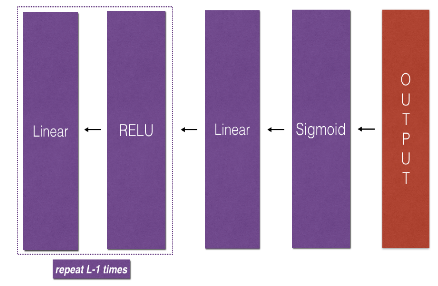
    • 重复[线性—>ReLU]前向传播函数 L-1 次（对于 1 到 L-1 层），再加上[线性—>sigmoid]在末尾（对于二元分类的最终层 L）。这形成了一个新的 L_model_forward 函数

  • 计算损失函数

  • 实现反向传播模块（下图中的红色部分）

    • 计算某一层的反向传播函数步骤的线性部分
    • 计算激活函数的梯度（relu_backward/sigmoid_backward）
    • 组合之前的两步形成一个新的[线性—>激活]反向传播函数
    • 重复[线性—>relu]反向传播 L-1 次，然后加上[线性—>sigmoid]反向传播在末尾。这形成了一个新的 L_model_backward 函数

  • 更新参数

初始化

两层神经网路初始化

  • 模型结构为：LINEAR -> RELU -> LINEAR -> SIGMOID
  • 权重 W 采用随机初始化
  • 偏差 b 采用初始化为零的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 单隐层神经网络的初始化
def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer
    
    Returns:
    parameters -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    W1 = np.random.randn(n_h,n_x)*0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h)*0.01
    b2 = np.zeros((n_y,1))

    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

L 层的神经网络的初始化

假设输入 X 维度是（12288，209），则其他的维度如下：

  • 模型结构为：[LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID
  • 权重 W 采用随机初始化
  • 偏差 b 采用初始化为零
  • 将每层单元个数储存在 list 变量 layer_dims 里面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# L 层神经网络的初始化
def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- 包含每一层的维度数据的list数组
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """
   
    parameters = {}    # 先建立一个空的参数dict
    L = len(layer_dims)   # 神经网络的总层数L 
    
    # 将参数 W1，b1，W2，b1... 初始化
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

    return parameters

前向传播模块

  • 线性前向传播
  • 线性—>激活前向传播，其中激活函数可以是 ReLU 或者 sigmoid
  • 整个模型为：[线性 —> relu] ×（L-1）—> 线性 —> sigmoid

线性前向传播

  • 输入上一层的激活值 A_prev，这一层的参数 W，b，
  • 输出这一层的线性值 Z 和 “线性缓存”
  • “线性缓存”是一个值为 (A_prev,W,b) 的 tuple
  • $Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 线性前向传播
def linear_forward(A_prev, W, b):
    """
    Arguments:
    A_prev -- 之前层的激活值 (或输入数据): (size of previous layer, number of examples)
    W -- 权重矩阵: numpy array of shape (size of current layer, size of previous layer)
    b -- 偏差向量, numpy array of shape (size of the current layer, 1)

    Returns:
    Z -- 这一层激活函数的输入值，也叫“前激活”参数 
    cache -- “线性缓存”，值为 (A_prev,W,b) 的 tuple，可以更有效率地计算反向传播
    """
    
    # 计算 Z 值
    Z = np.dot(W,A_prev) + b
    
    assert(Z.shape == (W.shape[0], A_prev.shape[1]))
    cache = (A_prev, W, b)	# “线性缓存”
    
    return Z, cache

一层线性-激活前向传播

  • 输入上一层的激活值 A_prev，这一层的参数 W 和 b，以及激活函数名 (字符串)
  • 输出这一层的激活值 A 和 “前向传播缓存”
  • “前向传播缓存” = “线性缓存”(A_prev,W,b) + “激活缓存”Z，是一个值为 ( (A_prev,W,b), Z) 的 tuple，简称“缓存”
  • $A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 一层线性-激活前向传播
def linear_activation_forward(A_prev, W, b, activation):
    """
    Arguments:
    A_prev -- 之前层的激活值 (或输入数据): (size of previous layer, number of examples)
    W -- 权重矩阵: numpy array of shape (size of current layer, size of previous layer)
    b -- 偏差向量, numpy array of shape (size of the current layer, 1)
    activation -- 在这一层用到的激活函数, 用字符串储存: "sigmoid" 或 "relu"

    Returns:
    A -- 这一层的激活值 
    cache -- 前向传播缓存，是一个包含 "linear_cache"（线性缓存，A_prev，W，b） 和 "activation_cache"（激活缓存，Z） 的 tuple：((A_prev,W,b),Z)
    """
    
    # 判断激活函数是 sigmoid 还是 relu
    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev,W,b)	# 先得到这一层的线性值 Z 和“线性缓存” (A_prev,W,b)
        A, activation_cache = sigmoid(Z)	# 再将 Z 激活得到 A 和“激活缓存” Z
    
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev,W,b) 	# 同理
        A, activation_cache = relu(Z)
    
    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)	# 将线性缓存和激活缓存合并成一个“前向传播缓存” tuple

    return A, cache

其中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# sigmoid 函数和 relu 函数
def sigmoid(Z):

    A = 1/(1+np.exp(-Z))
    cache = Z 	# 激活缓存 Z
    
    return A, cache

def relu(Z):
    
    A = np.maximum(0,Z)
    
    assert(A.shape == Z.shape)
    
    cache = Z	# 激活缓存 Z
    return A, cache

L 层模型的前向传播

对于二元分类，先 [线性-relu激活] L-1 次，再 [线性-sigmoid激活] 一次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 二元分类 L 层模型的前向传播
def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
    
    Arguments:
    X -- 初始训练集, numpy array of shape (input size, number of examples)
    parameters -- 初始化函数 initialize_parameters_deep() 输出的初始化之后的参数
    
    Returns:
    AL -- 最终层即 L 层的激活值
    caches -- 包含每一层"前向传播缓存"的 list (一共有 L-1 个, 索引值为 0 到 L-1)
              其中每一层的缓存是一个 tuple：((A,W,b),Z)
    """

    caches = []
    A = X
    L = len(parameters) // 2	# 神经网络的层数，由于参数有 W 和 b，故要除以 2
    
    # 实现 [线性 -> RELU] 前向传播 L-1 次，并把每一次的缓存加到总缓存 caches 中.
    for l in range(1, L):
        A_prev = A 
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], 'relu')	# 切记是 'relu'字符串 而不是 relu
        caches.append(cache)	# 将每一次的缓存加入总缓存 caches
    
    # 实现 [线性 -> sigmoid] 前向传播 1 次，并把这一次的缓存加到总缓存 caches 中.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid')
    caches.append(cache)
    
    assert(AL.shape == (1,X.shape[1]))
            
    return AL, caches

关于缓存，在对输入进行线性运算时，生成“线性缓存”，是一个 (A_prev,W,b) 的 tuple，在对线性值进行激活运算时，生成“激活缓存”，是一个值为 Z 的数组，在进行 [线性-激活] 的前向传播时，生成的是“前向传播缓存”，简称“缓存”，是一个值为 ((A_prev,W,b),Z) 的 tuple

计算代价函数

1
2
3
4
5
6
7
8
9
10
11
# 计算代价函数
def compute_cost(AL, Y):
  
    m = Y.shape[1]	# 总样本个数

    cost = -1/m * ( np.dot(Y, np.log(AL).T) + np.dot((1-Y), np.log(1-AL).T) )

    cost = np.squeeze(cost)      # 确保代价函数是一个数而不是数组 (e.g. this turns [[17]] into 17).
    assert(cost.shape == ())
    
    return cost

反向传播模块

  • 线性反向传播
  • 线性—>激活反向传播，其中“激活”计算 relu 或者 sigmoid 函数的梯度
  • 整个模型为：[线性 —> relu] ×（L-1）—> 线性 —> sigmoid

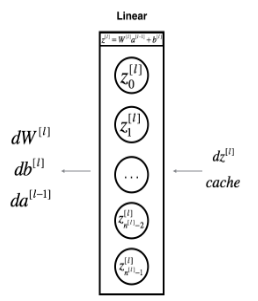
线性反向传播

已知 $dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}}$ 和该层 “线性缓存”(A_prev,W,b)，求 $dW^{[l]}, db^{[l]} ,dA^{[l-1]}$ ，如下图所示

计算公式为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 线性反向传播
def linear_backward(dZ, cache):
    """
    Arguments:
    dZ -- 代价函数对某l层线性输出 Z 的偏导 (of current layer l)
    cache -- 该l层的前向传播“线性缓存” tuple：(A_prev, W, b)

    Returns:
    dA_prev -- 代价函数对前一层 l-1 层的激活值的偏导数，与 A_prev 的形状相同
    dW -- 代价函数对当前层 l 层的权重 W 的偏导数，形状与 W 相同
    db -- 代价函数对当前层 l 层的偏差 b 的偏导数，形状与 b 相同
    """
    A_prev, W, b = cache	# 将该层“线性缓存”提取出来
    m = A_prev.shape[1]		# 总样本数m

    # 根据公式计算 dW，db，dA_prev
    dW = 1/m * np.dot(dZ, A_prev.T)
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)
    
    return dA_prev, dW, db

一层线性-激活反向传播

  • 已知 $dA^{[l]} = \frac{\partial \mathcal{L} }{\partial A^{[l]}}$ 和 $g(.)$ 和该层 “前向传播缓存”((A_prev,W,b),Z)，先求 $dZ^{[l]}$, 再求 $dW^{[l]}, db^{[l]} ,dA^{[l-1]}$
  • $dZ^{[l]} = dA^{[l]} * g’(Z^{[l]})$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 一层线性-激活反向传播
def linear_activation_backward(dA, cache, activation):
    """
    Arguments:
    dA -- 当前层l层的激活值梯度 
    cache -- “前向传播缓存”tuple：((A_prev,W,b),Z)
    activation -- 在这一层用到的激活函数, 用字符串储存: "sigmoid" 或 "relu"
    
    Returns:
    dA_prev -- 代价函数对前一层 l-1 层的激活值的偏导数，与 A_prev 的形状相同
    dW -- 代价函数对当前层 l 层的权重 W 的偏导数，形状与 W 相同
    db -- 代价函数对当前层 l 层的偏差 b 的偏导数，形状与 b 相同
    """
    linear_cache, activation_cache = cache	# 从“前向传播缓存”中提取“线性缓存”和“激活缓存”
    
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)	# 先用 dA 求得 dZ
        dA_prev, dW, db = linear_backward(dZ, linear_cache)	  # 再运行线性反向传播
        
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)		#同理
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    
    return dA_prev, dW, db

其中 dA 求得 dZ 的函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def relu_backward(dA, cache):
    """
    实现单个 relu 单元的反向传播

    Arguments:
    dA -- 某l层的激活值
    cache -- 该层的“激活缓存” Z

    Returns:
    dZ -- 代价函数对l层的 Z 的梯度
    """
    
    Z = cache	# 将 Z 值从“激活缓存”取出
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    
    # 根据 relu 函数，当 Z<=0，dZ 也为零
    dZ[Z <= 0] = 0
    
    assert (dZ.shape == Z.shape)
    
    return dZ

def sigmoid_backward(dA, cache):
    
    Z = cache
    
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)
    
    assert (dZ.shape == Z.shape)
    
    return dZ

L 层模型的反向传播

对于二元分类，先 [sigmoid—>线性] 一次，再 [relu—>线性] L-1 次

  • 反向传播初始化，即求 dAL 可以使用公式：$dAL=-\frac{Y}{AL}-\frac{1-Y}{1-AL}$
  • 将梯度数据存入名为 grads 的 dict 中：$grads[“dW” + str(l)] = dW^{[l]}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# L 层模型的反向传播
def L_model_backward(AL, Y, caches):
    """
    Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
    
    Arguments:
    AL -- 前向传播的最终激活值向量
    Y -- 真实的“标签”向量 (包含 0 if non-cat, 1 if cat)
    caches -- 总缓存，包含每一层的“前向传播缓存”，用 sigmoid 函数进行激活的缓存是 cache[L-1]，用 relu 函数进行激活的缓存是 cache[l] (for l in range(L-1),即 l = 0,1...,L-2)
    
    Returns:
    grads -- 包含代价函数对 A,W,b 的梯度的 dict
             grads["dA" + str(l)] = ... 
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ... 
    """
    grads = {}	# 先建立一个储存梯度的空 dict
    L = len(caches)	# 神经网络的总层数
    m = AL.shape[1]	# 训练集样本的个数
    Y = Y.reshape(AL.shape) # 让 Y 和 AL 的形状相同
    
    # 反向传播的初始化，即求 dAL
    dAL =  - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))	# 逐元素相除
    
    # 第 L 层先 [sigmoid -> 线性] 反向传播一次. 输入：dAL, current_cache. 输出：grads["dAL-1"], grads["dWL"], grads["dbL"]
    current_cache = caches[L-1]	  #从总缓存 caches 中取出当前缓存 
    grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, 'sigmoid')	 # 进行一次反向传播，，并把dAL-1，dWL，dbL 放入字典中
    
    # 继续反向传播，从 l=L-2 循环到 l=0，故从 l+1 开始
    for l in reversed(range(L-1)):	  # 将 range() 倒序
        # 第 l 层: [relu -> 线性] 反向传播求梯度.
        # 输入：grads["dA" + str(l + 1)], current_cache. 输出：grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        current_cache = caches[l]	# 取出当前层的缓存
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads['dA' + str(L-1)], current_cache, 'relu')	# 输入的是 dAL-1
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp

    return grads

更新参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 用梯度下降更新参数
def update_parameters(parameters, grads, learning_rate):
    """
    Arguments:
    parameters -- 包含所有初始化后的参数的字典
    grads -- 包含所有参数的梯度的字典
    learning_rate -- 学习率
    
    Returns:
    parameters -- 包含所有更新过的参数的字典
                  parameters["W" + str(l)] = Wl 的值
                  parameters["b" + str(l)] = bl 的值
    """
    
    L = len(parameters) // 2	# 神经网络的层数

    # 用公式更新参数
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]

    return parameters

第二部分：图片识别应用

这是深度学习专项课程第一课第四周的编程作业的第二部分，通过这一部分，可以学到：

  • 学习如何使用第一部分中构建的辅助函数来建立我们需要的任何结构的模型
  • 用不同的模型结构进行实验观察每一种的表现
  • 认识到在从头开始构建神经网络之前构建辅助函数使得任务更加容易

包的引入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v3 import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

数据集

数据集包括：

  • m_train 个训练集，包括图片集 train_set_x_orig 和标签集 train_set_y
  • m_test 个测试集，包括图片集 test_set_x_orig 和标签集 test_set_y
  • 每张图片都是方形 (height = num_px, width = num_px)，有三个颜色通道，所以数组形状是 (num_px, num_px, 3)
  • 每个图片集都要进行预处理，所以原始数据加上 _orig，但是标签集不需要预处理

数据集预处理

加载原始数据集

1
2
# 加载数据集
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
1
2
3
4
5
# 测试
index = 1
plt.imshow(train_set_x_orig[index]) # 画图
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") +  "' picture.")
# np.squeeze() 用于把一个数组的 shape 中为 1 的维度删掉，即让 train_set_y[:, index] 变为一个数

确定图片维度和个数以防止出错

  • 训练集的个数：m_train
  • 测试集的个数：m_test
  • 图片（正方形）的尺寸即边长的像素数：num_px
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 确定维度和个数
# train_set_x_orig 形状为 (m_train, num_px, num_px, 3)
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]

print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
1
2
3
4
5
6
7
8
>>Number of training examples: m_train = 209
  Number of testing examples: m_test = 50
  Height/Width of each image: num_px = 64
  Each image is of size: (64, 64, 3)
  train_set_x shape: (209, 64, 64, 3)
  train_set_y shape: (1, 209)
  test_set_x shape: (50, 64, 64, 3)
  test_set_y shape: (1, 50)

重构图片数组变为标准输入矩阵

把尺寸为 (num_px, num_px, 3) 的图片变为 shape 为 (num_px ∗ num_px ∗ 3, 1) 的向量

把一个 shape 为 (a,b,c,d) 的矩阵变为一个 shape 为 (b∗c∗d, a) 的矩阵的技巧：x_flatten = X.reshape(X.shape[0], -1).T

实际上，reshape() 是按行取元素，按行放元素

1
2
3
4
5
6
7
8
9
# 重构图片数组
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T

print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))#重构后完整性检查
1
2
3
4
5
>>train_set_x_flatten shape: (12288, 209)
  train_set_y shape: (1, 209)
  test_set_x_flatten shape: (12288, 50)
  test_set_y shape: (1, 50)
  sanity check after reshaping: [17 31 56 22 33]

数据标准化

为了使得数据在一个合适的尺度上，我们需要将数据标准化，对于图片来说，由于图片的每个像素的 RGB 值介于 0 到 255 之间，所以我们可以将每个特征值除以 255，这样就能将它们标准化了

1
2
3
# 数据标准化
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.

一般方法

  • 初始化参数 / 定义超参数

  • 进行 num_iterations 次循环：

    • 前向传播
    • 计算代价函数
    • 反向传播
    • 更新参数

  • 用训练过的参数来预测标签值

两层的神经网络构建

会用到的之前构建的函数有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def initialize_parameters(n_x, n_h, n_y):
    ...
    return parameters 
def linear_activation_forward(A_prev, W, b, activation):
    ...
    return A, cache
def compute_cost(AL, Y):
    ...
    return cost
def linear_activation_backward(dA, cache, activation):
    ...
    return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

确定每层的单元数：

1
2
3
4
n_x = 12288     # 输入向量维度
n_h = 7		# 隐藏层单元数
n_y = 1		# 输出层单元数
layers_dims = (n_x, n_h, n_y)

将构建的函数组合起来形成主函数：

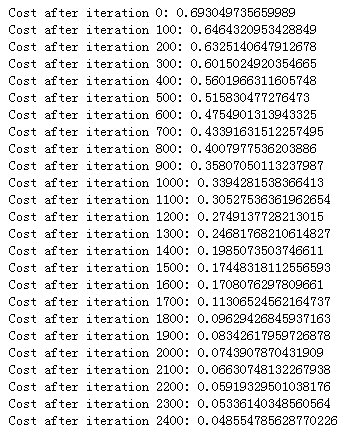
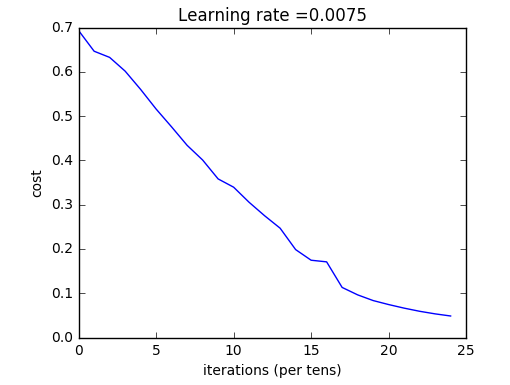
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    实现一个两层的神经网络: LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- 输入数据, of shape (n_x, number of examples)
    Y -- 真实的标签向量 (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- 每一层的单元数 (n_x, n_h, n_y)
    num_iterations -- 梯度下降的迭代次数
    learning_rate -- 梯度下降学习率
    print_cost -- 如果值为 True 则每一百步打印一次代价函数
    
    Returns:
    parameters -- 包含更新后的参数 W1，W2，b1，b2 的字典
    """

    grads = {}
    costs = []	# 用来记录每百步的代价函数的值
    m = X.shape[1]	# 样本数
    (n_x, n_h, n_y) = layers_dims
    
    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    # 参数字典中取出 W1，W2，b1，b2
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 梯度下降循环 num_iterations 次
    for i in range(0, num_iterations):
        # 前向传播，输出下一层的激活值和“前向传播缓存”
        A1, cache1 = linear_activation_forward(X, W1, b1, 'relu')
        A2, cache2 = linear_activation_forward(A1, W2, b2, 'sigmoid')
        
        # 计算代价函数
        cost = compute_cost(A2, Y)
        
        # 反向传播初始化，即求得 dAL
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        # 反向传播，获得前一层的激活值梯度和这一层的参数梯度
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, 'sigmoid')
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, 'relu')
        
        # 将参数梯度都存入 grads 字典
        grads['dW1'] = dW1
        grads['db1'] = db1
        grads['dW2'] = dW2
        grads['db2'] = db2
        
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
       
        # 从参数字典中取出参数并赋值以便下一次迭代
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        # 每百步打印一次代价函数
        if print_cost and i % 100 == 0:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if print_cost and i % 100 == 0:
            costs.append(cost)	# 方便等下打印图表
       
    # 打印出代价函数的图表
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters	# 返回更新过的参数

用我们的数据集进行测试：

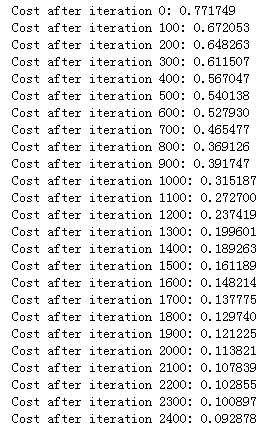
1
parameters = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)

看看预测训练集的精确度：

1
predictions_train = predict(train_x, train_y, parameters)

>> Accuracy: 1.0

再看看预测测试集的精确度：

1
predictions_test = predict(test_x, test_y, parameters)

>> Accuracy: 0.72

我们可以看到比第二周的逻辑回归的 70% 的精确度要稍高，接下来我们建立一个 L 层的神经网络进行试验。

L 层的神经网络

可以用到的之前构建的函数有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def initialize_parameters_deep(layers_dims):
    ...
    return parameters 
def L_model_forward(X, parameters):
    ...
    return AL, caches
def compute_cost(AL, Y):
    ...
    return cost
def L_model_backward(AL, Y, caches):
    ...
    return grads
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

确定每层的单元数：

1
layers_dims = [12288, 20, 7, 5, 1]	# 这是一个四层的模型

将辅助函数组合到主函数中：

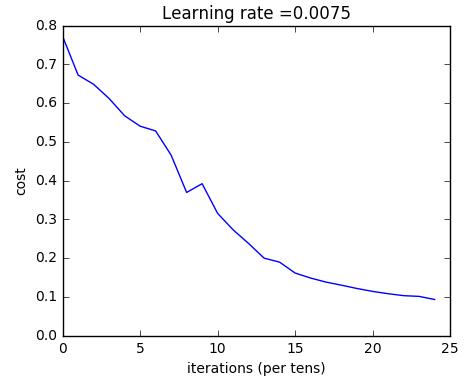
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    实现一个 L 层的神经网络: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
    
    Arguments:
    X -- 输入数据向量, numpy array of shape (number of examples, num_px * num_px * 3)
    Y -- 真实的标签向量 (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- 包含输入向量维度和每层的单元数的列表, 长度为层数 + 1
    learning_rate -- 梯度下降学习率
    num_iterations -- 梯度下降循环迭代次数
    print_cost -- 若为 True，则每百步打印一次代价函数 cost
    
    Returns:
    parameters -- 模型训练出来的参数，可用于预测标签值
    """

    costs = []	# 用来记录代价函数
    
    # 参数初始化
    parameters = initialize_parameters_deep(layers_dims)
    
    # 梯度下降循环
    for i in range(0, num_iterations):
        # 前向传播: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        AL, caches = L_model_forward(X, parameters)	  # 注意在前向传播的过程中会得到总缓存 caches
        
        # 计算代价函数
        cost = compute_cost(AL, Y)
    
        # 反向传播
        grads = L_model_backward(AL, Y, caches)	  # 注意反向传播时要用上前向传播的总缓存 caches
 
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
       
        # 每百步打印一次代价函数值
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
            
    # 画出代价函数图表
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

用数据集训练模型试试看：

1
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)

得到的结果如下：

看看预测训练集的精确度：

1
pred_train = predict(train_x, train_y, parameters)

>> Accuracy: 0.985645933014

看看预测测试集的精确度：

1
pred_test = predict(test_x, test_y, parameters)

>> Accuracy: 0.8

我们可以看到 4 层神经网络的 80% 精确度比逻辑回归的 70% 和 2 层神经网络的 72% 精确度要高很多！

还可以拿自己的图片进行预测：

1
2
3
4
5
6
7
8
9
10
11
12
# 首先将自己的图片加到 image 文件夹
my_image = "my_image.jpg" # 将这个改成你图片的名字 
my_label_y = [1] # 图片的真实标签值 (1 -> cat, 0 -> non-cat)

fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((num_px*num_px*3,1))
my_image = my_image/255.
my_predicted_image = predict(my_image, my_label_y, parameters)

plt.imshow(image)
print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")

找了十张动物图片来进行测试，前五张不是猫，后五张是猫，测试结果是：第一张熊猫识别错误，第二张北极熊识别错误，第三张大象识别正确，第四张兔子识别正确，第五张非洲狮识别正确（其实对这张最没信心，因为外形和猫实在是太像了，反而识别正确了==），第六张猫识别错误，第七张猫识别错误，第八张猫识别正确，第九张猫识别正确，第十张猫识别正确，粗略看来，这十张图的正确率有六成，模型仍需改进！

结果分析

试着打印出分类错误的图片：

1
print_mislabeled_images(classes, test_x, test_y, pred_test)

我们可以发现有以下特征的图片更难判断正确：

  • 猫的身体在不寻常的位置
  • 猫的颜色与背景颜色相似
  • 特殊的猫的颜色和种类
  • 相机角度
  • 图片的明亮度
  • 大小变化（猫在图片中很大或者很小）
吴恩达深度学习笔记AI神经网络
微信捐赠
支付宝捐赠