本周主要介绍深度神经网络 (Deep Neural Networks)。
深度神经网络概况
什么是深度神经网络
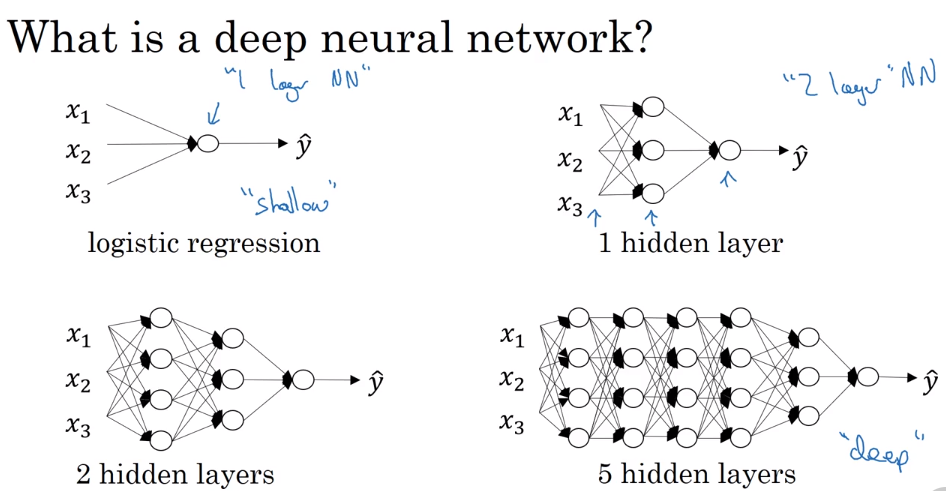
所谓深浅取决于神经网络的层数,例如左上角的逻辑回归模型是一个“最浅的”神经网络,而右下角的神经网络具有五个隐藏层,可以算得上是深度神经网络。
神经网络的符号含义
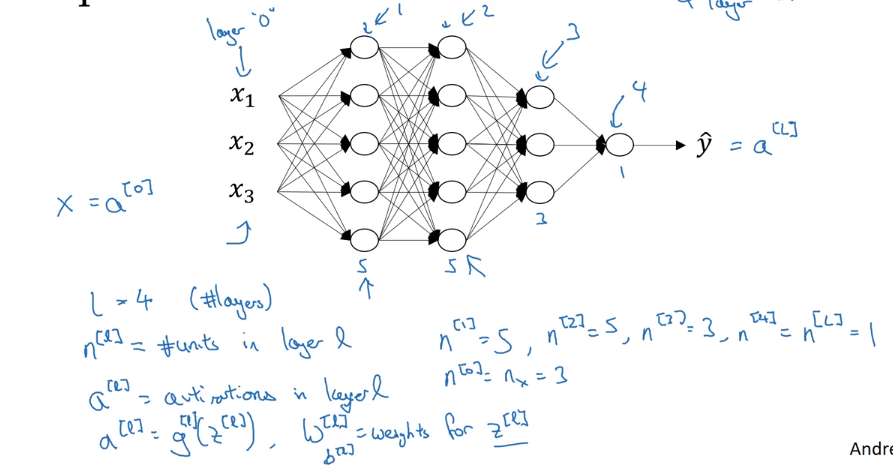
- l —— 表示神经网络的层数
- $n^{[l]}$ 表示 l 层的单元数,图中 $n^{[0]}=n_x=3,n^{[1]}=5,n^{[2]}=5,n^{[3]}=3,n^{[4]}=n^{[l]}=1$
- $a^{[l]}=g^{[l]}(z^{[l]})$ 表示 l 层的激活向量
- $W^{[l]}$ 表示产生 l 层的权重
- $b^{[l]}$ 表示产生 l 层的偏差
为什么我们需要“深度”
例子1 —— 面部识别
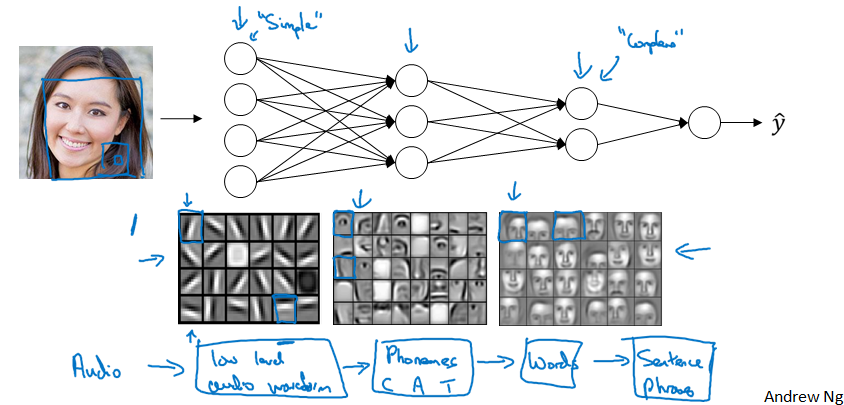
神经网络的第一层可以被认为是一个边缘检测器,这一层的神经元正试图找到人脸的边缘在哪里,通过将像素分组的方法形成边缘,然后取消边缘检测,并将边缘组合在一起,形成面部的一部分,最后将面部的不同部位组合在一起我们可以识别不同的面部,我们可以将神经网络的浅层当作简单的检测函数,然后后一层将他们组合在一起,以便我们可以学习更复杂的功能
例子2 —— 电路理论
用一个隐藏神经元数量较少但是具有深度的神经网络来计算某些函数时,如果我们尝试用浅层神经网络来计算同样的函数,则需要指数级的隐藏神经元来进行计算。
建立深度神经网络的基本框架
框架的建立过程
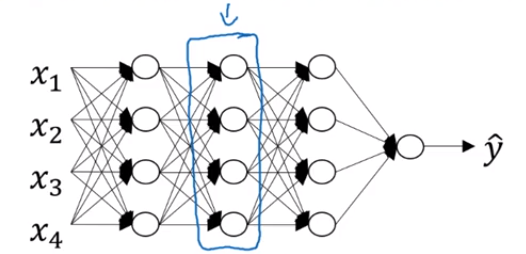
假设方框中的隐藏层为第 l 层:
参数:$W^{[l]},b^{[l]}$
前向传播:输入 $a^{[l-1]}$ ,输出 $a^{[l]}$,缓存 $z^{[l]}$
反向传播:输入 $da^{[l]}$ 和缓存 $z^{[l]}$,输出 $da^{[l-1]}$,$dW^{[l]}$,$db^{[l]}$
画成框图如下所示:
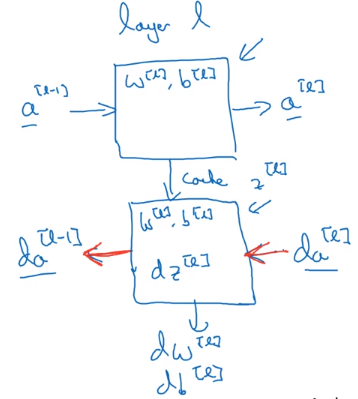
总体框架
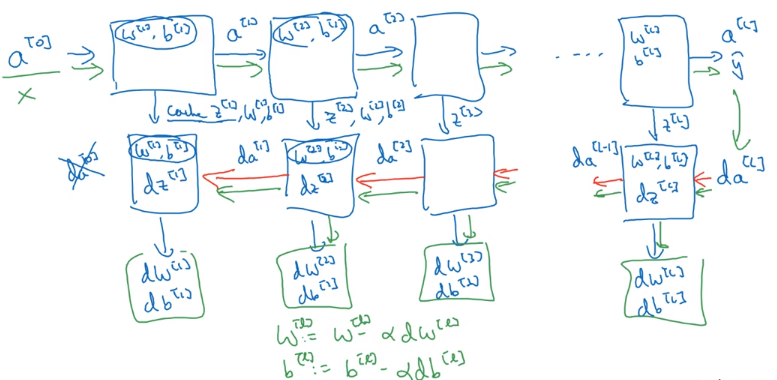
前向传播
公式
输入 $a^{[l-1]}$ ,输出 $a^{[l]}$,缓存 $z^{[l]}$
非向量化
向量化
$X=A^{[0]} → A^{[1]}→A^{[2]}→…→ A^{[l]}$
维度的确定
有如下的一个5层的神经网络:
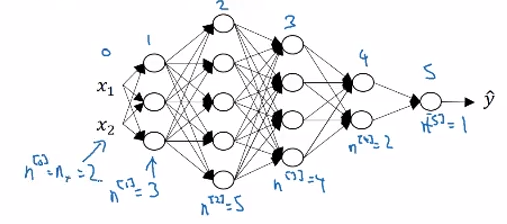
对于单个训练样本:
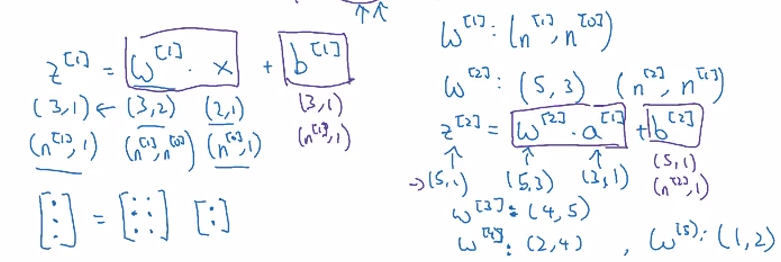
$z^{[l]},dz^{[l]},a^{[l]},da^{[l]}:(n^{[l]},1)\\W^{[l]},dW^{[l]}:(n^{[l]},n^{[l-1]})\\b^{[l]},db^{[l]}:(n^{[l]},1)$
对于多个训练样本:
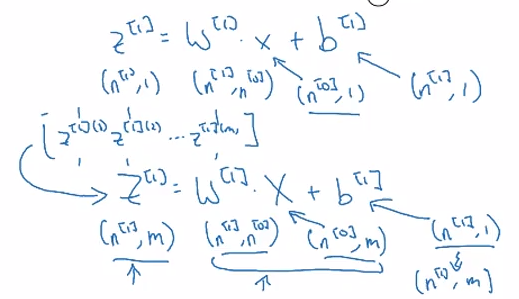
$ Z^{[l]},dZ^{[l]},A^{[l]},dA^{[l]}:(n^{[l]},m)\\W^{[l]},dW^{[l]}:(n^{[l]},n^{[l-1]})\\b^{[l]},db^{[l]}:(n^{[l]},1)$
其中 $l=0$ 时,$A^{[0]}=X=(n^{[0]},m)$
反向传播
公式
输入 $da^{[l]}$ 和缓存 $z^{[l]}$,输出 $da^{[l-1]}$,$dW^{[l]}$,$db^{[l]}$
非向量化
向量化
参数 (parameters) 与超参数 (hyperparameters)
定义
什么是参数:$W^{[1]},b^{[1]},W^{[2]},b^{[2]},W^{[3]},b^{[3]}…$
什么是超参数:学习率 (learning rate) $\alpha$ ,迭代次数 (iterations),隐藏层数 (hidden layers) L,隐藏单元数 (hidden units) $n^{[1]},n^{[2]}…$ ,激活函数 (activation function) 的选择,动量,最小批大小,各种形式的正则化参数等等,由于这些参数都会影响参数 W 和 b 的最终结果,所以我们称之为超参数
深度学习是一个基于试验的过程
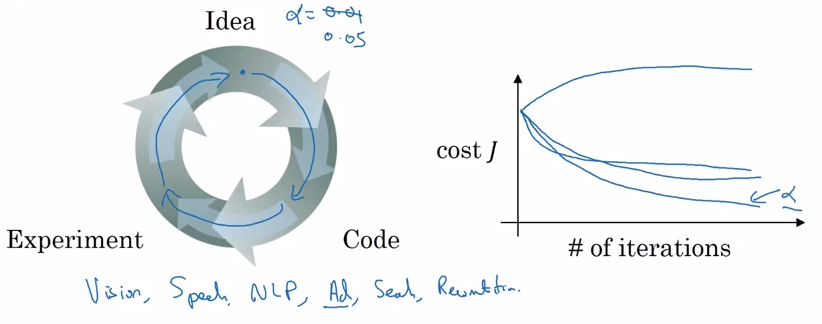
深度学习和大脑有什么关系
吴恩达:深度学习和大脑相似度并不高,但深度学习和大脑的确有某些可以对比的地方,如下图,但是人脑中的神经元是如何进行学习的还是一个迷,而且至今我们还不清楚到底人脑中有没有一个类似于反向传播或者梯度下降的算法



