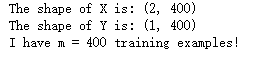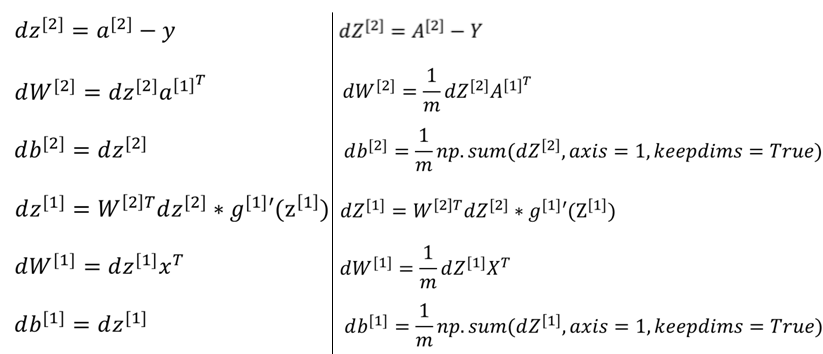艺琛的 Livehouse主页学习笔记读书观影笔记个人随想爱好和生活相册所有博客特色标签关于我
coursera 吴恩达深度学习 Specialization 编程作业（course 1 week 3）
|学习笔记

这是深度学习专项课程第一课第三周的编程作业，通过这次编程作业，可以学到：

  • 用一个单隐层神经网络实现一个二元分类器
  • 使用非线性的激活函数
  • 计算交叉熵损失
  • 实现前向和后向传播

包的引入

1
2
3
4
5
6
7
8
9
10
11
12
# 引入包
import numpy as np 
import matplotlib.pyplot as plt # 画图
from testCases_v2 import * # 提供测试例子评估函数正确性
import sklearn # 提供简单有效的数据挖掘和数据分析工具
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets # 提供一些有用的函数

%matplotlib.inline

np.random.seed(1) # 使得每次生成的随机数都和第一次相同

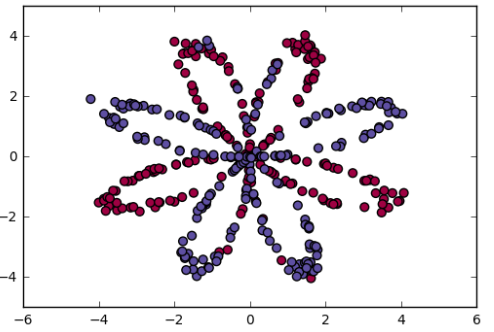
数据集

加载数据

1
2
# 加载一个花朵形状的二分类数据集进 X 和 Y
X, Y = load_planar_dataset()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
> # load_planar_dataset 的具体代码
> def load_planar_dataset():
>     np.random.seed(1)
>     m = 400 # number of examples
>     N = int(m/2) # number of points per class
>     D = 2 # dimensionality
>     X = np.zeros((m,D)) # data matrix where each row is a single example
>     Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
>     a = 4 # maximum ray of the flower
> 
>     for j in range(2):
>         ix = range(N*j,N*(j+1))
>         t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
>         r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
>         X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
>         Y[ix] = j
>         
>     X = X.T
>     Y = Y.T
> 
>     return X, Y
>

数据可视化

1
2
# 数据可视化
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.spectral) # 画散点图，其中参数 c 是颜色索引值，s 是尺寸，cmap 是颜色索引方式

　确定数据维度

1
2
3
4
5
6
7
8
# 确定数据集的尺寸
shape_X = np.shape(X)
shape_Y = np.shape(Y)
m = X.shape[1] # 训练集尺寸

print('the shape of X is:' + str(shape_X))
print('the shape of Y is:' + str(shape_Y))
print('I have m = %d training examples!' %(m))

用 sklearn 库实现简单的逻辑回归

1
2
3
# 训练逻辑回归分类器
clf = sklearn.linear_model.logisticRegressionCV() # 建立一个逻辑回归的对象 clf
clf.fit(X.T, Y.T) # 用数据集拟合模型，返回一个训练过的模型对象，注意数据集的尺寸为 (n_samples, n_features)，所以要进行转置
1
2
3
# 打印逻辑回归的边界
plot_decision_boundary(lambda x: clf.predict(x),X,Y)
plt.title("Logistic Regression")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
> def plot_decision_boundary(model, X, y):
>     # 设置图形最大最小值
>     x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
>     y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
>     h = 0.01
>     # np.meshgrid() 形成间隔为 h 的点阵
>     xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
>     # 预测点阵的标签值
>     Z = model(np.c_[xx.ravel(), yy.ravel()]) # np.c_[] 按行连接两个矩阵，ravel() 把多维数组变成一维数组
>     Z = Z.reshape(xx.shape)
>     # 生成等高线图像
>     plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral) # 生成等高线图并添加颜色
>     plt.ylabel('x2')
>     plt.xlabel('x1')
>     plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
>
1
2
3
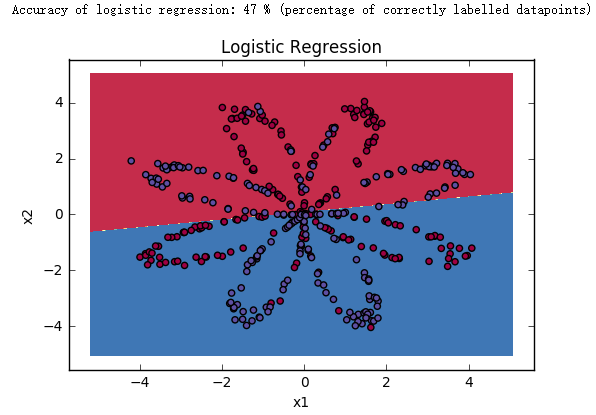
# 打印精确度
LR_predictions = clf.predict(X.T) # 用模型预测的 X 的标签值
print('Accuracy of logistic regression: %d ' % float( (np.dot(Y,LR_prediction) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) + '%' + "(percentage of correctly labelled datapoints)")

我们可以发现使用逻辑回归进行预测的准确度非常低！

神经网络模型

建立神经网络的一般方法

  • 定义神经网络结构，包括输入特征个数，隐藏神经元个数等
  • 初始化模型参数
  • 循环以下步骤：
    • 实现前向传播
    • 计算代价函数
    • 实现反向传播，得到梯度
    • 使用梯度下降更新参数
  • 将所有辅助函数合并到一个主函数 nn_model() 中

定义神经网络结构

1
2
3
4
5
6
7
8
# 确定 n_x n_h n_y 三个变量
def layer_sizes(X, Y):
    
    n_x = X.shape[0] # 计算输入层的尺寸
    n_h = 4 # 计算隐藏层的尺寸，即隐藏神经元个数
    n_y = Y.shape[0] # 计算输出层的尺寸
    
    return (n_x, n_h, n_y)

初始化模型参数

注意：

  • 确保所有参数的尺寸正确
  • 对于权重 W 采用随机初始化的方法
  • 对于偏差 b 采用初始化为零的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 参数的初始化
def initialize_parameters(n_x, n_h, n_y):
    
    W1 = np.random.randn(n_h, n_x)*0.01 # 0.01 使得初始化后的参数更小，梯度下降更快，W1(n_h, n_x)
    b1 = np.zeros((n_h,1)) # 切记是 np.zeros(()),b1(n_h,1)
    W2 = np.random.randn(n_y, n_h)*0.01 # W2(n_y, n_h)
    b2 = np.zeros((n_y,1)) # b2(n_y,1)
    
    # 确保参数唯独正确
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h,1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    # 将参数值放入字典 parameters
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

前向传播

步骤：

  • 从 parameters 字典中取出每个参数
  • 实现前向传播，计算 Z1,A1,Z2,A2 的值
  • 把这些值放在字典 cache 中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 前向传播
def forward_propagation(X, parameters):
    
    # 把参数从 parameters 取出来
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 计算Z1 Z2 A1 A2 的值
    Z1 = np.dot(W1,X) + b1
    A1 = np.tanh(Z1) # numpy 内置的 tanh() 函数
    Z2 = np.dot(W2,A1) + b2
    A2 = sigmoid(Z2) # sigmoid 已经 imported
    
    # 确保 A2 的尺寸正确
    assert(A2.shape == (1, X.shape[1]))
    
    # 把求到的值放入字典 cache
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

计算代价函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 计算代价函数
def compute_cost(A2, Y, parameters):
    
    m = X.shape[1]
    
    # 计算
    logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1-A2), (1-Y)) # np.multiply() 为逐元素相乘
    cost = -(1/m)*np.sum(logprobs)
    
    # 确保 cost 的维度是我们需要的，比如把 [[17]] 变成 17
    cost = np.squeeze(cost)
    assert(isinstance(cost,float))
    
    return cost

反向传播

  • 因为 $g^{[1]}(z) = tanh(z)$ ， 所以 $g^{[1]’}(z) = 1-a^2$，所以可以使用 (1 - np.power(A1, 2)) 来计算 $g^{[1]’}(Z^{[1]})$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 反向传播
def back_propgation(parameters, cache, X, Y):
    
    m = X.shape[1]
    
    # 首先将 W1 和 W2 从 parameters 里取出来,将 A1 和 A2 从 cache 里取出来
    W1 = parameters["W1"]
    W2 = paramaters["W2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    
    # 计算梯度
    dZ2 = A2 - Y
    dW2 = (1/m)*np.dot(dZ2,A1.T)
    db2 = (1/m)*np.sum(dZ2,axis=1,keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T,dZ2),(1-np.power(A1,2)))
    dW1 = (1/m)*np.dot(dZ1,X.T)
    db1 = (1/m)*np.sum(dZ1,axis=1,keepdims=True)
    
    # 将数据存入 grads 中
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

梯度下降

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 梯度下降法更新数据
def update_parameters(parameters, grads, learning_rate = 1.2):
    
    # 首先将参数从 parameters 中取出来
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 然后将梯度从 grads 中取出来
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    
    # 更新参数，此处只更新一次参数
    W1 = W1 - learning_rate*dW1
    b1 = b1 - learning_rate*db1
    W2 = W2 - learning_rate*dW2
    b2 = b2 - learning_rate*db2
    
    # 将更新后的参数放到 parameters 中
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

将以上所有辅助函数合并到主函数中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 主函数
def nn_model(X, Y, n_h, num_iteration = 10000, print_cost=False ):
    # 定义模型结构
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sized(X, Y)[2]
    
    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)
    
    # 将参数取出
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 梯度下降迭代
    for i in range(0, num_iterations):
        # 前向传播
        A2, cache = forword_propagation(X, paramaters)
        # 计算代价函数
        cost = compute_cost(A2, Y, parameters)
        # 反向传播
        grads = backward_propagation(parameters, cache, X, Y)
        # 梯度下降更新参数
        parameters = update_parameters(parameters, grads, learning_rate = 1.2)
        
        # 每千步打印一次 cost 值
        if print_cost and i % 1000 == 0：
        	print("Cost after iteration %i: %f" %(i, cost))
    
    return parameters

用模型进行预测

如果最后的预测值大于 0.5，则标签值为 1，反之标签值为 0

1
2
3
4
5
6
7
8
9
def predict(parameters, X):
	
    # 调用前向传递函数进行预测
    A2, cache = forward_propagation(X,parameters)
    predictions = (A2 > 0.5) 
    # predictions = np.where(A2 > 0.5, 1, 0)
    # numpy.where(condition, x, y)当 conditon 的某个位置的为 true 时，输出 x 的对应位置的元素，否则选择 y 对应位置的元素；
    
    return predictions

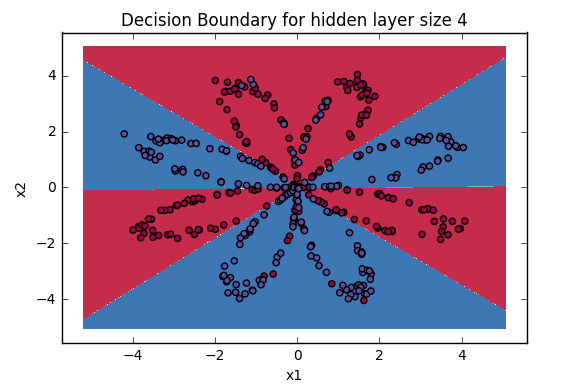
分析讨论

当隐藏节点个数为 4 时

1
2
3
4
5
6
7
8
9
10
# 建立 n_h = 4 的模型
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)

# 打印出分类边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

# 打印出精确度
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))  /  float(Y.size)*100) + '%')

我们可以看到对比逻辑回归，四个隐藏节点的神经网络模型的预测精确度非常高！

接下来我们看看不同隐藏节点对预测结果的影响。

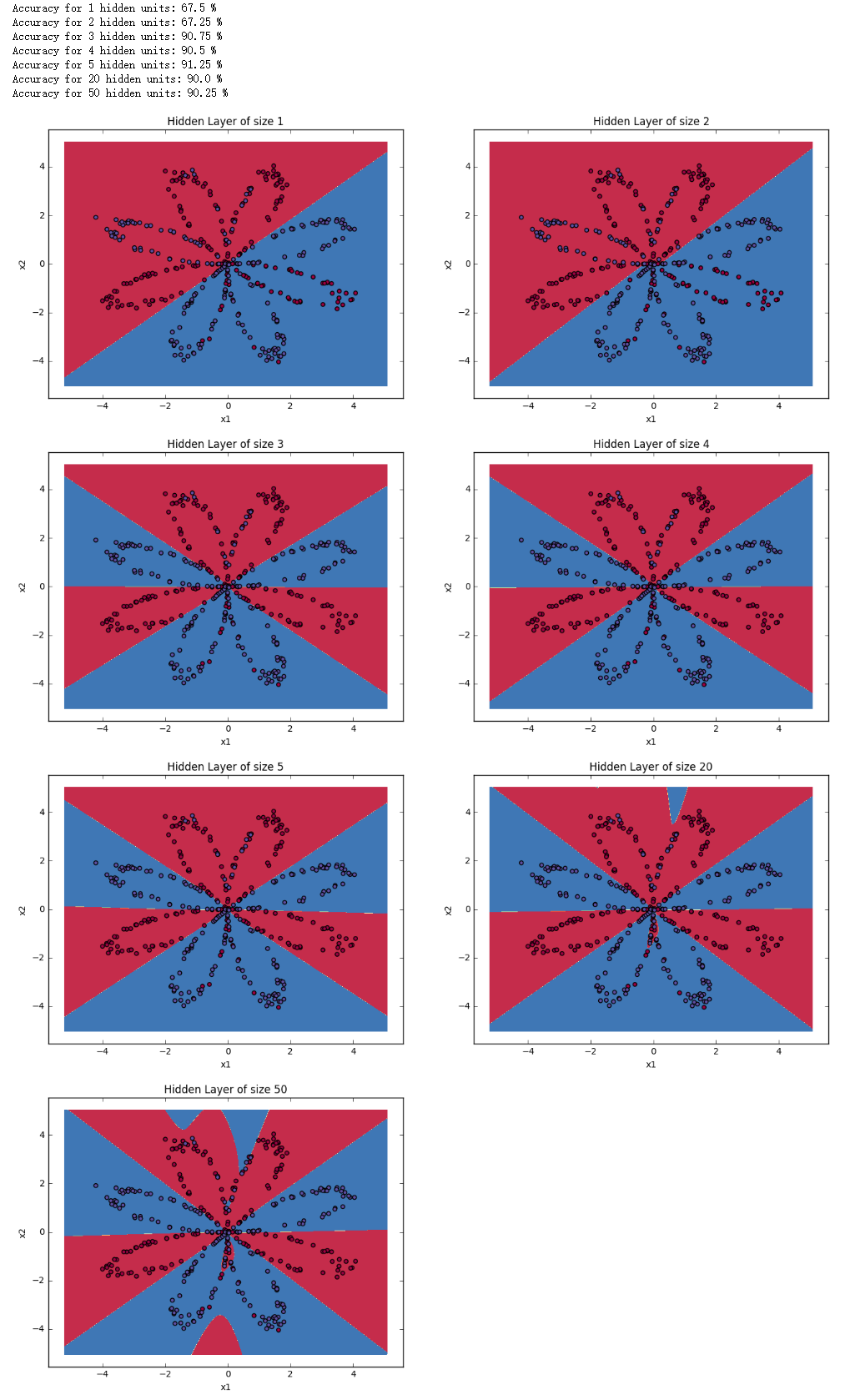
改变隐藏节点个数观察结果

1
2
3
4
5
6
7
8
9
10
11
# 打印不同隐藏节点模型的预测结果
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] # 不同隐藏节点个数
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

得出结论

  • 隐藏节点的个数越多，对数据集的拟合程度越好，直到最终发生过拟合
  • 最好的隐藏节点个数似乎大概在 5 个左右，在这个值附近的的模型对数据集拟合得很好且没有发生过拟合
  • regularization 是减小大型模型（比如 n_h = 50）过拟合的一个方法，在后面会学到

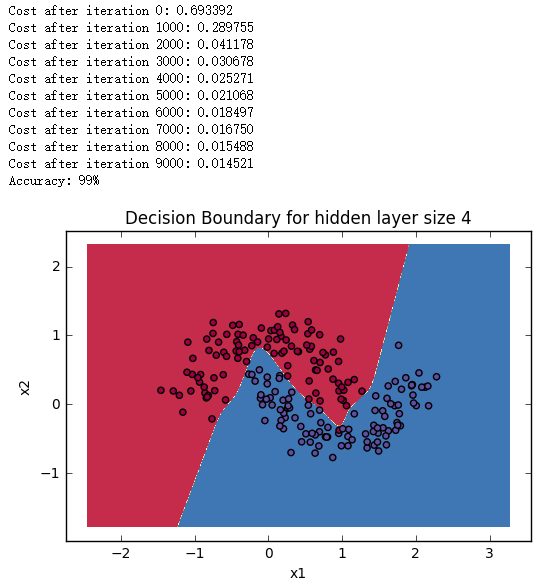
更换其他数据集进行试验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 数据集
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()

datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

dataset = "noisy_circles" # 选择数据集

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

# make blobs binary
if dataset == "blobs":
    Y = Y%2

# 数据可视化
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);

# 建立模型
parameters = nn_model(X, Y, n_h = 5, num_iterations = 10000, print_cost=True)

# 画出分类边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

# 打印精确度
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

吴恩达深度学习笔记AI神经网络
微信捐赠
支付宝捐赠