本周主要介绍单隐层神经网络 (one hidden layer Neural Network)。

神经网络概况

什么是神经网络

逻辑回归的计算图如下，这是一个最小的神经网络：

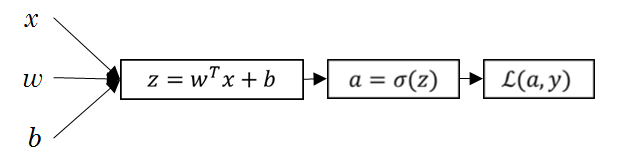
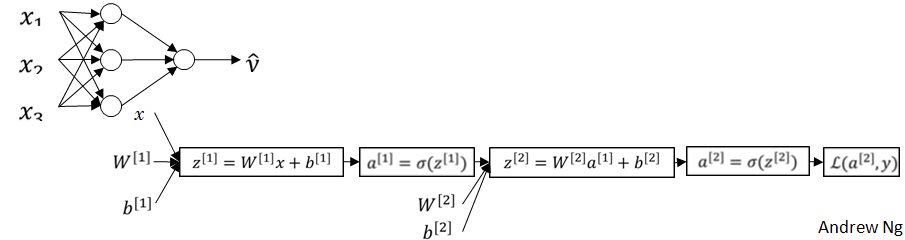
堆叠一系列的 $\sigma$ 单元，构建一个单隐层神经网络：

神经网络的含义

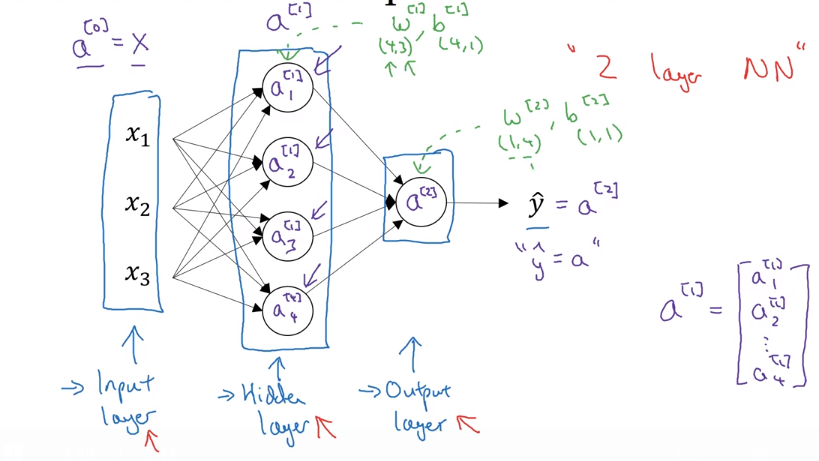
• 第一个方框称之为 输入层 (Input layer) ，这一层的激活向量用 $a^{[0]}$ 表示，$x = a^{[0]}$，其中字母 a 表示 activate(激活值)
• 第二个方框称之为 隐藏层 (Hidden layer )，这一层的激活向量用 $a^{[1]}$ 表示
• 第三个方框称之为 输出层 (Output layer)，这一层的激活向量用 $a^{[2]}$ 表示，$\hat y = a^{[2]}$
• 神经网络的层数用右上角的方括号表示，输入层不算入层数
• 第一层的参数为 $W^{[1]} (4,3)$ 和 $b^{[1]} (4,1)$
• 第二层的参数为 $W^{[2]} (1,4)$ 和 $b^{[2]} (1,4)$
• 每个圆圈称之为 节点 (node)

神经网络的前向传播及其向量化

非向量化公式

在逻辑回归中一个圆圈代表两步运算，如下图所示：

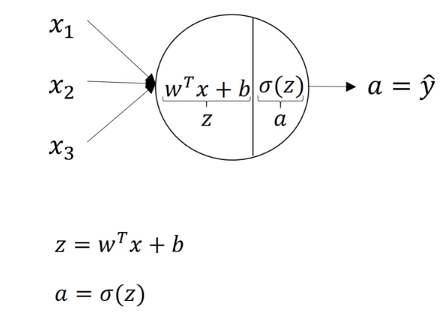
在神经网络中每个圆圈也代表两步运算，将圆圈隔离出来看便是一个逻辑回归模型，如图所示：

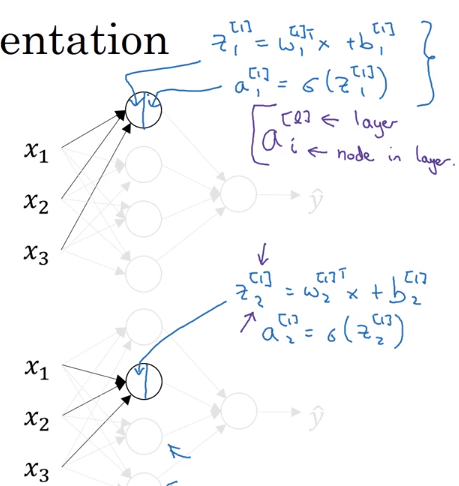
整理成如下的样子：

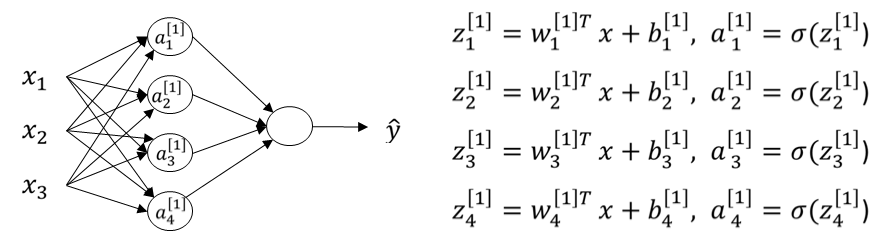
单训练样本的向量化

已知：

$$z^{[1]}_1 = w^{[1]T}_1 x + b^{[1]}_1, a^{[1]}_1= \sigma (z^{[1]}_1) \\ z^{[1]}_2 = w^{[1]T}_2 x + b^{[1]}_2, a^{[1]}_2= \sigma (z^{[1]}_2) \\ z^{[1]}_3 = w^{[1]T}_3 x + b^{[1]}_3, a^{[1]}_3= \sigma (z^{[1]}_3) \\ z^{[1]}_4 = w^{[1]T}_4 x + b^{[1]}_4, a^{[1]}_4= \sigma (z^{[1]}_4) \\$$

推导：

$$z^{[1]}=\begin{bmatrix} z^{[1]}_1\\ z^{[1]}_2\\ z^{[1]}_3\\ z^{[1]}_4 \end{bmatrix}= \begin{bmatrix} w^{[1]T}_1x+b^{[1]}_1\\ w^{[1]T}_2x+b^{[1]}_2\\ w^{[1]T}_3x+b^{[1]}_3\\ w^{[1]T}_4x+b^{[1]}_4 \end{bmatrix}= \begin{bmatrix} --& w^{[1]T}_1 &-- \\ --& w^{[1]T}_2 &-- \\ -- & w^{[1]T}_3 & --\\ --& w^{[1]T}_4 & -- \end{bmatrix}_{(4,3)} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}+ \begin{bmatrix} b^{[1]}_1\\ b^{[1]}_2\\ b^{[1]}_3\\ b^{[1]}_4 \end{bmatrix}=W^{[1]}x + b^{[1]}$$ $$a^{[1]}=\begin{bmatrix} a^{[1]}_1\\ a^{[1]}_2\\ a^{[1]}_3\\ a^{[1]}_4 \end{bmatrix}=\sigma (z^{[1]})$$

最后得到计算神经网络前向传播的四个公式：

$$z^{[1]}=W^{[1]}x+b^{[1]} =W^{[1]}a^{[0]}+b^{[1]}\\ a^{[1]}=\sigma (z^{[1]}) \\ z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} \\ a^{[2]}=\sigma (z^{[2]}) \\$$

注意：

$$\begin{bmatrix} --& w^{[1]T}_1 &-- \\ --& w^{[1]T}_2 &-- \\ -- & w^{[1]T}_3 & --\\ --& w^{[1]T}_4 & -- \end{bmatrix}_{(4,3)}=W^{[1]} \neq W^{[1]T}$$

这里与逻辑回归中有所不同，参数 $W^{[1]} (4,3)$ 和 $W^{[2]} (1,4)$ 的右上角没有转置符号，所有的参数 w 都成了行向量而不是列向量，也就是说 $W^{[2]}$ 相当于逻辑回归中的 $w^T$

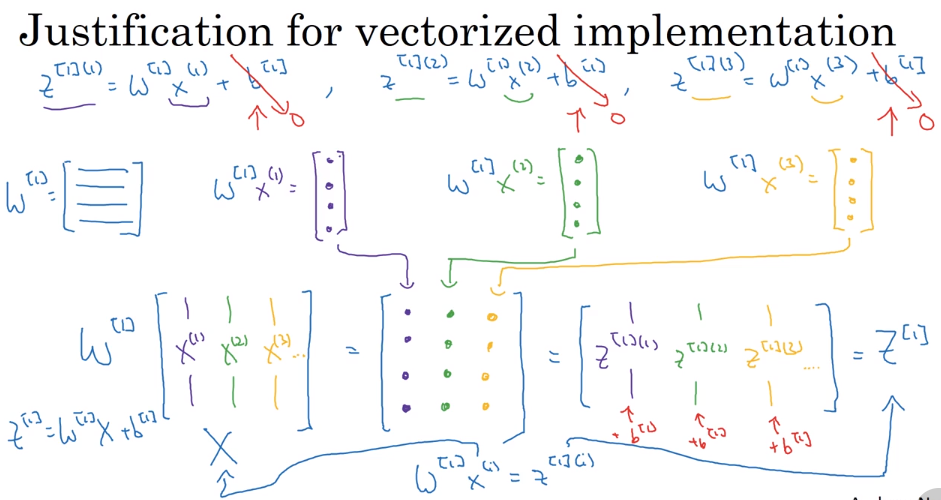
多个训练样本的向量化

1. 记法：

对于第 i 个训练样本的预测值我们记为：$\hat y^{(i)} = a^{ [2] (i)}$，其中 [2] 表示第二层，(i) 表示第 i 个训练样本。

为了输出所有样本的预测值，我们可以遍历所有的样本：

$for i = 1 \quad to \quad m: \\ \quad z^{[1] (i)}=W^{[1]} x^{(i)}+b^{[1]} =W^{[1]} a^{[0] (i)}+b^{[1]} \\ \quad a^{[1] (i)}=\sigma (z^{[1] (i)}) \\ \quad z^{[2] (i)}=W^{[2]} a^{[1] (i)}+b^{[2]} \\ \quad a^{[2] (i)}=\sigma (z^{[2] (i)}) $

1. 公式：

$$Z^{[1]}=W^{[1]}X+b^{[1]}\\ A^{[1]}=\sigma (Z^{[1]})\\ Z^{[2]}=W^{[2]}A^{[2]}+b^{[1]}\\ A^{[2]}=\sigma (Z^{[2]})\\$$

其中：

$$Z^{[1]}= \begin{bmatrix} | &| & &| \\ z^{[1](1)}& z^{[1](2)} & ... & z^{[1](m)}\\ |& | & &| \end{bmatrix}\quad A^{[1]}= \begin{bmatrix} | &| & &| \\ a^{[1](1)}& a^{[1](2)} & ... & a^{[1](m)}\\ |& | & &| \end{bmatrix}\quad X^{[1]}= \begin{bmatrix} | &| & &| \\ x^{[1](1)}& x^{[1](2)} & ... & x^{[1](m)}\\ |& | & &| \end{bmatrix}\\$$ $$Z^{[2]}= \begin{bmatrix} | &| & &| \\ z^{[2](1)}& z^{[2](2)} & ... & z^{[2](m)}\\ |& | & &| \end{bmatrix}\quad A^{[2]}= \begin{bmatrix} | &| & &| \\ a^{[2](1)}& a^{[2](2)} & ... & a^{[2](m)}\\ |& | & &| \end{bmatrix}\quad X^{[2]}= \begin{bmatrix} | &| & &| \\ x^{[2](1)}& x^{[2](2)} & ... & x^{[2](m)}\\ |& | & &| \end{bmatrix}\\$$

矩阵的横向代表不同的训练样本，纵向代表不同的隐藏节点 (hidden unit)

1. 推导过程：

激活函数

常见的激活函数

sigmoid 函数

$$sigmoid: g(z)=a=\frac {1}{1+e^{-z}}\\ \quad \quad \quad g'(z)=a(1-a)$$

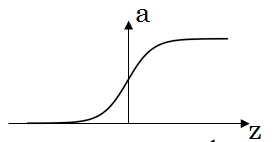
• 由于 tanh 函数比 sigmoid 函数更好，所以 sigmoid 函数只用在二元分类问题的输出层

tanh 函数

$$tanh：g(z)=a=\frac {e^{z}-e^{-z}}{e^{z}+e^{-z}}\\ \quad \quad \quad \quad \quad \quad \quad \quad g'(z)=1-(tanh(z))^2=1-a^2$$

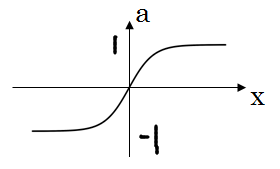
• 也叫双曲正切函数，是一个移位后重新调整比例使输出范围在 -1 到 1 之间的 sigmoid 函数
• sigmoid 函数使隐藏层输出的平均值逼近于 0.5 ，而 tanh 函数更加逼近 0，这样使得下一层的学习更加简单，所以 tanh 函数在大多数情况下都严格优于 sigmoid 函数
• 缺点是在 z 很大时，函数的斜率会接近 0 ，这样使得学习速率变得很慢

ReLU 函数

$$ReLU:g(z)=a=max\{0,z\}\\ \quad \quad \quad \quad g'(z)=\left\{\begin{matrix} 0 & &if \ z<0 \\ 1& & if \ z\geqslant 0 \end{matrix}\right.$$

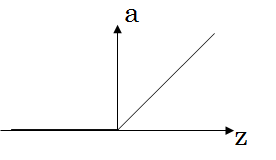
• 实际上当 z = 0 时导数无定义，但是工程上由于 z = 0 的概率无限小，所以 g’(0) 可以设为任意值
• 也叫线性整流函数
• 减少了激活函数导数趋向 0 的现象
• 隐藏层的激活函数的首选，用的最多

Leaky ReLU

$$Leaky ReLU:g(z)= a = max\{ 0.01z,z\}\\ \quad \quad \quad \quad \quad \quad \quad g'(z)=\left\{\begin{matrix} 0.01 & &if \ z<0 \\ 1& & if \ z\geqslant 0 \end{matrix}\right.$$

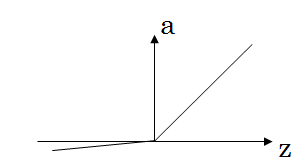
• 实际上当 z = 0 时导数无定义，但是工程上由于 z = 0 的概率无限小，所以 g’(0) 可以设为任意值
• 一般效果好于 ReLU，但是用的较少

为什么神经网络需要非线性激活函数

已知公式：

$z^{[1]}=W^{[1]} x+b^{[1]} \\ a^{[1]}=g^{[1]} (z^{[1]}) \\ z^{[2]}=W^{[2]} a^{[1]}+b^{[2]} \\ a^{[2]} = g^{[2]} (z^{[2]})$

假设 $g^{[1]} 和g^{[2]}$ 是线性激活函数：$g^{[1]}=g^{[2]}=z$

即：$a^{[1]}=z^{[1]}$，$a^{[2]}=z^{[2]}$

可以推导出：

$a^{[2]}=z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}=W^{[2]}z^{[1]}+b^{[2]}=W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}\\=(W^{[2]}W^{[1]})x+(W^{[2]}b^{[1]}+b^{[2]})=W’x+b’$

我们可以发现，当激活函数是线性函数时，不管神经网络有多少层，最后的输出值只是输入值的线性函数，这样还不如去除所有的隐藏层，因为我们可以看到最后的结果和逻辑回归模型一模一样，所以线性的隐藏层没有任何作用，线性函数的组合还是线性函数。

只有一种情况会用到线性激活函数，就是例如预测房价这类回归问题的输出层

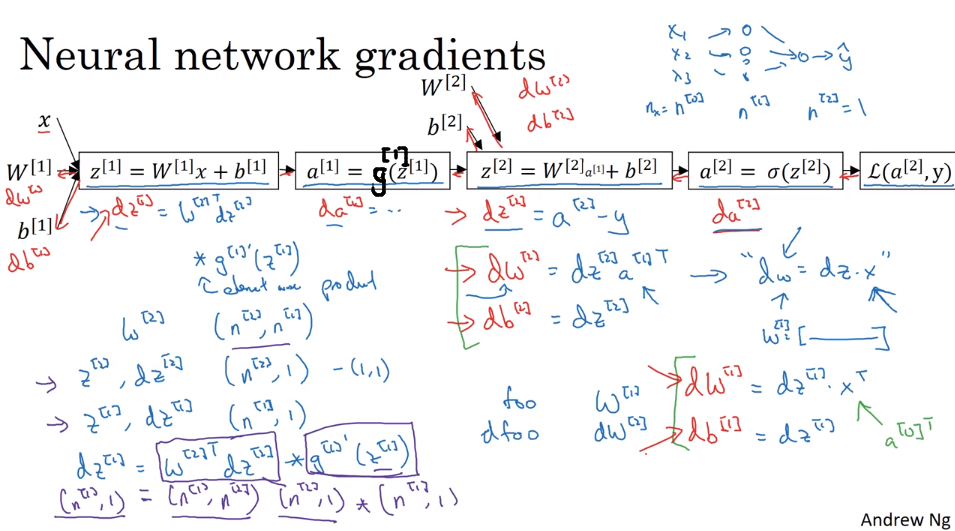
神经网络的反向传播及其向量化

概况

$输入: n_x=n^{[0]}, n^{[1]},n^{[2]}=1\\参数: W^{[1]} \rightarrow (n^{[1]},n^{[0]}),b^{[1]}\rightarrow (n^{[1]},1),W^{[2]} \rightarrow (n^{[2]},n^{[1]}),b^{[2]} \rightarrow (n^{[1]},1)\\ 代价函数：J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=\frac {1}{m} \sum\limits_{i=1}^nL(\hat y,y),\hat y=a^{[1]}\\梯度下降：\\ repeat:\{ \\ 计算预测值 \hat y,i=1,2…,m\\计算 dW^{[1]}=\frac {dJ}{dW^{[1]}}, db^{[1]}=\frac {dJ}{db^{[1]}},…\\ W^{[1]}:= W^{[1]}-\alpha dW^{[1]}\\b^{[1]}:= b^{[1]}-\alpha db^{[1]}\\W^{[2]}:= W^{[2]}-\alpha dW^{[2]}\\b^{[2]}:= b^{[2]}-\alpha db^{[2]}\\ \}$

向量化

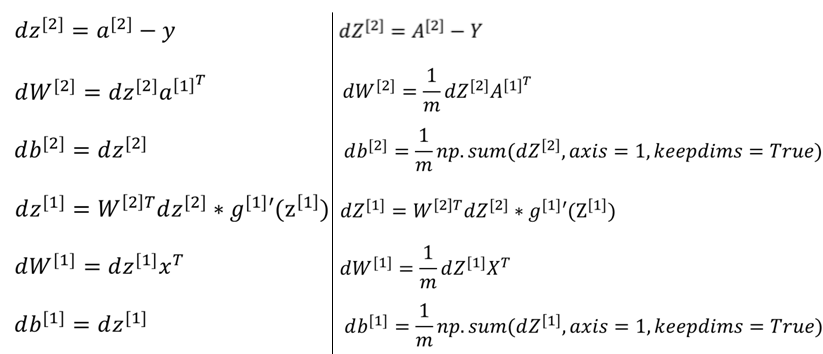
• 左边是单个训练样本的向量化，右边是多个训练样本的向量化
• keepdims = True 是为了保持输出我们需要的维度，防止出现秩为 1 的数组
• 第四行的 * 号代表 逐元素相乘
• 由于 W 的每个 w 都变成行向量，这点与逻辑回归不同，故第二行、第五行的 $a^{[1]T},x^T,A^{[1]T},X^T$ 都要加转置符号
• 只有当是二元分类时，第一行公式才成立
• $dZ^{[1]} \rightarrow (n^{[1]},m),W^{[2]T}dZ^{[2]} \rightarrow (n^{[1]},m),g^{[1]’}(Z^{[1]}) \rightarrow (n^{[1]},m)$

向量化的推导过程

参数的随机初始化

为什么不能将权重 W 全初始化为零

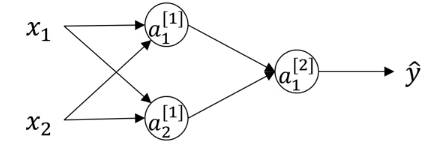
对于上面的的神经网络，我们假设将 $W^{[1]}$ 和 $b^{[1]}$ 全都初始化为零，正如我们在逻辑回归中做的那样，即 $W^{[1]}=\begin{bmatrix}0 &0 \\0 & 0\end{bmatrix}\quad b^{[1]}=\begin{bmatrix}0\\0\end{bmatrix}$ ，导致 $a^{[1]}_1=a^{[2]}_2$ ，在反向传播时有，$dz^{[1]}_1=dz^{[2]}_2$ ，于是 $dW=\begin{bmatrix}u&v \\u & v\end{bmatrix}$ ，由于 $W^{[1]}=W^{[1]}-\alpha dW$，所以 $W^{[1]}=\begin{bmatrix}a&b \\a & b\end{bmatrix}$，我们可以看到，无论迭代多少次，无论神经网络训练多久，这两个隐藏神经元的参数始终都相同，他们始终都在做相同的运算，称这两个神经元是对称的，不能给我们带来任何帮助。

参数随机初始化

$$W^{[1]}=np.random.randn((2,2))*0.01\\ b^{[1]}=np,zero((2,1))\\ W^{[2]}=np.random.randn((1,2))*0.01\\ b^{[2]}=0$$

数据 0.0.1 必须比较小，因为如果 W 非常大，那么 z 也相应会非常大，那么可以发现此处对应的激活函数比如 sigmoid 或者 tanh 函数的斜率会非常小，这意味着梯度下降得非常慢，所以应该使 W 为一个较小的值