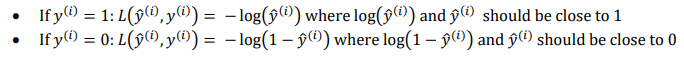coursera 吴恩达深度学习 Specialization 笔记（course 1 week 2）—— 神经网络基础

本周主要介绍逻辑回归算法 (Logistics Regression)。

二元分类

定义

输出值为离散的两个值，即 1 或者 0

例子——判断图片是（1）不是（0）猫

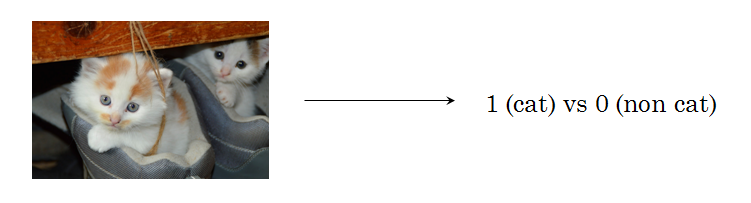
目标：输入图片的特征向量 x，预测对应的输出是 1 还是 0

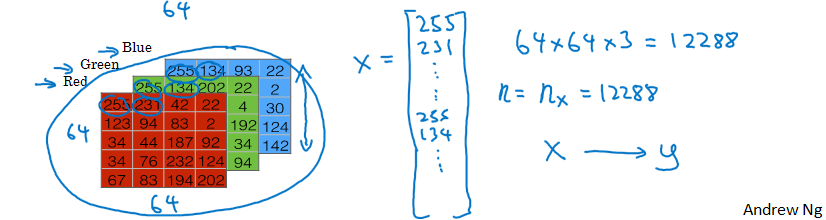
图片特征值的提取

图片特征值的提取：每张图片有三个颜色通道，把每个通道的所有像素值取出展成一个向量，每张图片（像素为 64*64）的所有特征值为 64x64x3 = 12288 个，组成一个维度为 12288 的列向量 X

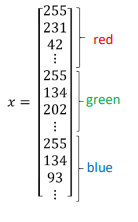
输入向量的维度 n = $n_x$= 12288

符号说明

逻辑回归 Logistics Regression（针对二元分类问题）

描述

逻辑回归是一个很小的神经网络，已知一个数据集，我们用它拟合出一个模型，这个模型能够实现：

输入特征值 $x$
输出预测值 $\hat y$： $\hat{y} = P(y = 1|x) , 0 \leq\hat{y} \leq1 $，即标签值 y = 1 的概率

那么如何得到某个输入 x 的标签值为 1 的概率呢，用如下式子来进行预测：

$\hat{y} = w^Tx + b$

但是由于概率的值在 0 和 1 之间，而 $w^T x+ b$ 可能大于 1 或者小于 0，所以这不是一个好的算法，于是我们将其通过一个 sigmoid函数 改造一下：

$\hat{y} =\sigma( w^Tx + b)$

输入特征向量 x： 𝑥 ∈ $ℝ^{n_x}$, 即 $x = \left ( x_{1},x_{2},x_{3},…,x_{n_x} \right )^T$,$n_x$ 为特征数目
训练标签 y：y $\in$ { 0 , 1 }
权重 w：$w = \left ( w_{1},w_{2},w_{3},…,w_{n_x} \right )^T$, $n_x$ 为特征数目
偏置量 b：实数
sigmoid 函数：$s=\sigma(z)=\frac{1}{1+e^{-z}}$

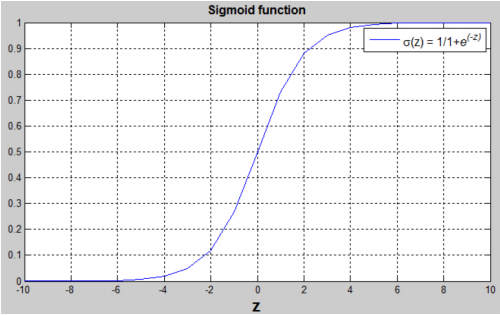
sigmoid 函数的合理性在于：

当 z 是一个很大的数时， $\sigma (z) = 1$

当 z 是一个很小的数时， $\sigma(z)=0$

当 z = 0 时，$\sigma(z)=0.5$

这样就能很好地估计介于 0 和 1 之间的概率

另外一种描述方式

$\hat{y} =\sigma( \Theta^Tx)$

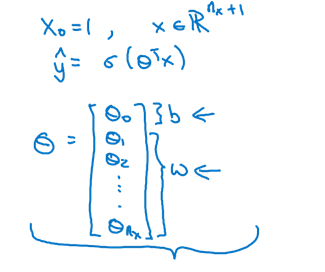
其中：

$x = (1,x_{1},x_{2},x_{3},…,x_{n_x})^T$
$\Theta = (b,w_{1},w_{2},w_{3},…,w_{n_x})^T$

损失函数（lost function）

为了训练参数 w 和 b，也就是找到最优的拟合模型，我们定义一个损失函数

　概括

右上角的括号 (i) 表示第 i 个训练实例

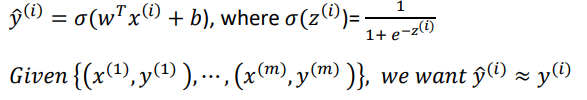
损失函数定义

损失函数评估了预测值 $\hat y^{(i)}$ 和已知的期望值 $y^{(i)}$ 之间的差异，或者说计算了单个训练样本的偏差

常用的损失函数

（1）

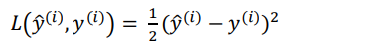
逻辑回归中一般不适用此损失函数，因为会使优化问题变成非凸问题，无法使用梯度下降法找到全局最优解

（2）

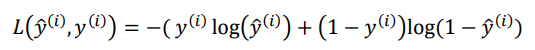
该损失函数的合理性在于：

代价函数（Cost function）

代价函数指的是整个训练集的损失函数的平均值，我们的最终目的就是找到使整个代价函数值最小的参数 w 和 b

我们希望用 $\hat{y} =\sigma( w^Tx + b)$ 模型得出的预测值和已知的实际值之间的差异最小，也就是代价函数最小，这样才能证明这个模型（假设参数为 $w_{best},b_{best}$）是所有包含参数 w，b 的模型里最合理的，也是最符合实际的

从输入到求得代价函数的过程称之为前向传播 (forward propagation)

代价函数：

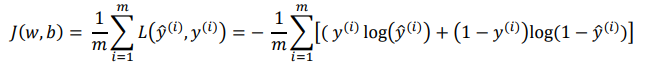
代价函数的证明

二元分类问题类似于概率论里的“0-1分布”.

假设当结果为 1 的概率 $P(y=1|x)=\hat y$
则当结果为 0 的概率就是 $P(y=0|x)=1-\hat y$
则结果为 y（0或1）的概率为 $P(y|x)=\hat y^y(1-\hat y)^{1-y}$，可带入y=0或1进行检验，发现该式子正确
假设有一个容量为 m 的数据集（假设符合独立同分布），根据最大似然原理，我们要使得我们的假设的 $\hat y$ 最正确，最符合实际，那么必须满足使得“用 $\hat y$ 估计到的目前整个数据集的概率”最大（之所以越大越接近实际，是因为这些数据集已经存在，发生的概率便是 1），那么根据独立事件概率相乘原理：
“用 $\hat y$ 估计到的目前整个数据集的概率”为 $L(\hat y)=P(y^{(1)}|x^{(1)})P(y^{(2)}|x^{(2)})…P(y^{(m)}|x^{(m)})\\\quad\quad =\prod\limits_{i=1}^m P(y^{(i)}|x^{(i)})\\ \quad\quad =\prod\limits_{i=1}^m {({\hat y^{(i)}})} ^{y^{(i)}} ( 1 - {\hat y^{(i)}} )^{1- y^{(i)}} $
为了让 $L(\hat y)$ 最大，由于是连乘，我们让 $logL(\hat y)$ 最大，则 $logL(\hat y) = \sum\limits ^m_{i=1} y^{(i)}log{\hat y}^{(i)}+(1-y^{(i)})log(1-{\hat y}^{(i)})$
而代价函数必须要尽量小，所以我们将 $logL(\hat y)$ 取负号，即 $-\sum\limits ^m_{i=1} y^{(i)}log{\hat y}^{(i)}+(1-y^{(i)})log(1-{\hat y}^{(i)})$
为了让代价函数处于更好的尺度上，我们加上系数 1/m，即 $J(w,b)=-\frac{1}{m}\sum\limits ^m_{i=1} y^{(i)}log{\hat y}^{(i)}+(1-y^{(i)})log(1-{\hat y}^{(i)})$
代价函数的逻辑为：某个 w，b 算出的代价函数越小 → $L(\hat y)$ 越大 → 用其估计到的目前整个数据集的概率就越大 → 用 w，b 为参数的模型的估计距离实际情况就越接近 → 该模型就越准确

用梯度下降法训练参数 w 和 b

概括

已知：

模型 $\hat{y} =\sigma( w^Tx + b)$，其中 $\sigma(z)=\frac{1}{1+e^{-z}}$
代价函数

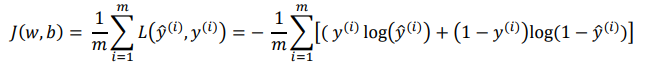
期望：

找到使 $J(w,b)$ 最小的 w 和 b，如图中红点所示，找到谷底的 w 和 b 值

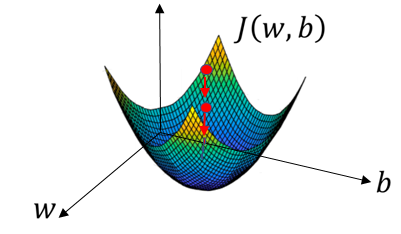
梯度下降法原理

用一些初始 w，b 值来初始化，通常用 0
朝着最陡的的下坡方向走一步，第一次迭代
第二次迭代
…
第 n 次迭代到达或接近全局最优点

单变量梯度下降法（先忽略b）

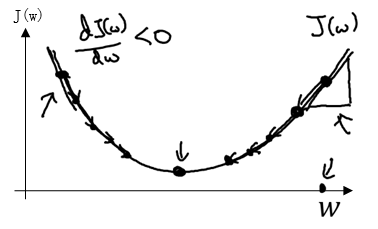
假设 J(w) 曲线如图中所示，为了找到谷底的 w 点，我们重复以下更新操作：

$w := w - \alpha\frac{dJ(w)}{dw}$

其中：

w : = 符号表示对 w 进行迭代更新
$\alpha$ 为学习率，控制每一次迭代的步长大小
在代码中导数 $\frac{dJ(w)}{dw}$ 的变量名写成 $dw$

多变量梯度下降法（w，b）

$J(w,b)$ $w := w - \alpha\frac{\partial J(w,b) }{\partial w}$ $b := b - \alpha\frac{\partial J(w,b) }{\partial b}$

求代价函数的导数

求损失函数的导数

已知公式：

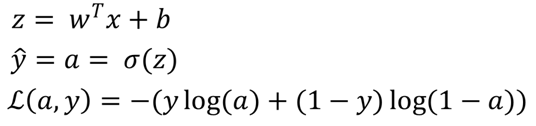
假设训练实例有两个特征 : $x_1,x_2$，则逻辑关系如下：

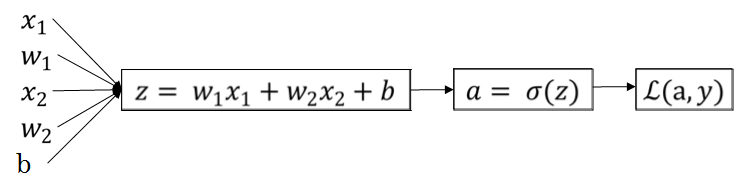
根据链式法则求偏导数，推导过程如下：

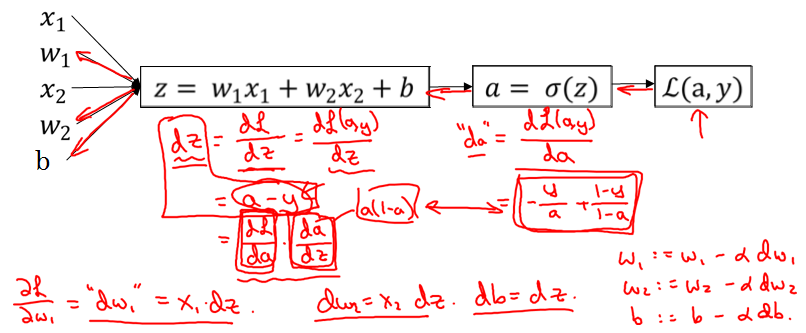
整理可得：

$“da”=\frac{dL}{da}= \frac {\partial L(a,y)}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}$ $“dz”= \frac {dL}{dz}=\frac{dL}{da}\frac{da}{dz}=a-y$ $“dw_1”=\frac{\partial L}{\partial w_1}=x_1dz$ $“dw_2”=\frac{\partial L}{\partial w_2}=x_2dz$ $“db” = \frac{\partial L}{\partial b} = dz$

其中：$“da””dz””dw_1””dw_2””db”$ 表示损失函数对其导数在 python 中的变量名，这个过程叫做 反向传播 (back propagation)

求代价函数的导数

由于代价函数是所有训练样本损失函数的平均值，故我们可以用如下的伪代码求得 $dw_1,dw_2,db$ (我们仍然假设只有两个特征值)：

首先初始化 $J=0;dw_1=0;dw_2=0;db=0$

遍历整个训练集：

For i = 1 to m:

$z^{(i)}=w^Tx^{(i)}+b\\a^{(i)}=\sigma(z^{(i)})\\J+=-[y^{(i)}loga^{(i)}+(1-y^{(i)})log(1-a^{(i)})]\\dz^{(i)}=a^{(i)}-y^{(i)}\\dw_1+=x_1^{(i)}dz^{(i)}\\dw_2+=x_2^{(i)}dz^{(i)}\\dw_3…\\dw_4… \\ …\\db+=dz^{(i)}$

最后除以训练集个数：

$J=J/m\\”dw_1”=\frac {\partial J}{\partial w_1}=dw_1/m\\”dw_2”=\frac {\partial J}{\partial w_2}=dw_2/m \\ … \\”db”=\frac {\partial J}{\partial b}=db/m$

我们可以看到为了求取代价函数的导数，我们需要进行两次遍历，这是一种十分低效的遍历方式，我们可以使用向量化（Vectorization）的方式加速我们的运算

最后用求得的代价函数的导数更新我们的参数：

$w_1:=w_1-\alpha dw_1\\w_2:=w_2-\alpha dw_1 \\ …\\b:=b-\alpha db$

向量化（Vectorization）

什么是向量化

是一门让代码变得高效的艺术
遍历是非向量化，而向量化充分利用 CPU 和 GPU 的并行化实现更快的运算

大概是指直接让两个向量或者矩阵进行点乘

向量化的好处

比非向量化计算效率快很多很多，下面的测试显示快 300 多倍
只要可能，尽量避免使用显式的 for 循环

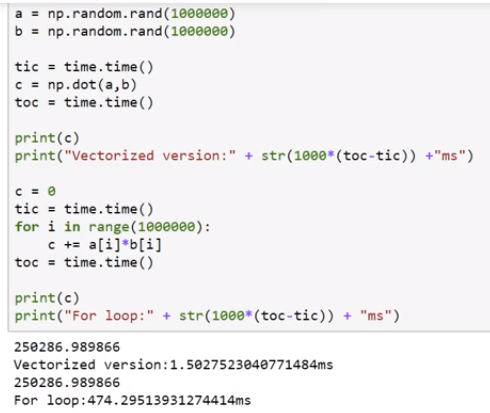
一些向量化的例子

计算 $u = A_{i \times j}V_{j \times 1}$

(1) 非向量化：

u = np.zero((n,1))
for i ...
    for j ...
    	u[i] += A[i][j]*v[j]

(2) 向量化：

1	u = np.dot(A,V)

计算某个向量所有元素的指数

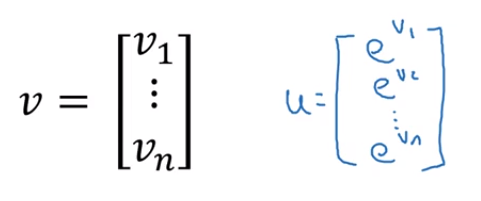
(1) 非向量化

1
2
3

u = np.zeros((n,1))
for i in range(n)
	u[i] = math.exp(V[i])

(2) 向量化

1 2	import numpy as np u = np.exp(V)

其他例子

np.log(V)
np.abs(V)
np.maximum(V)
V**2
1/V

用向量化实现逻辑回归

用 for 循环实现

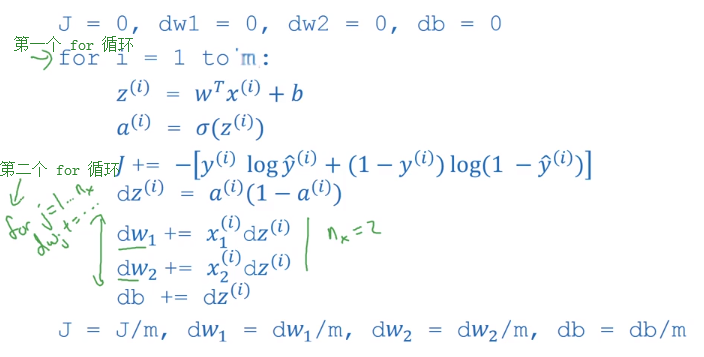
向量化实现

前向传播

求取 Z：

$Z=[z^{(1)}\quad z^{(1)}\quad…\quad z^{(m)}]\\=[w^Tx^{(1)}+b\quad w^Tx^{(2)}+b\quad …\quad w^Tx^{(m)}+b] \\=w^T[x^{(1)}\quad x^{(1)}\quad …\quad x^{(m)}]+[b\quad b\quad…\quad b]\\=w^TX+[b\quad b\quad…\quad b]$

实现代码为：
1
Z = np.dot(w.T,X) + b
此处 b 为一个实数，但是 numpy 会自动将这个实数 b 拓展为一个 1 乘 m 的行向量，这个在 python 中称为 广播（broadcasting）

求取 A：

$A=[a^{(1)} \ a^{(2)} \ … \ a{(m)}]= \sigma(Z)$
反向传播

求取 dZ：

$dZ=[dz^{(1)} \ dz^{(2)} \ … \ dz^{(m)}]\\=[a^{(1)}-y^{(1)} \quad a^{(1)}-y^{(1)} \ … \quad a^{(m)}-y^{(m)}]\\=A -Y $

其中 $Y=[y^{(1)}\quad y^{(2)}\quad … \quad y^{(m)}]$

求取 dw：

$dw=\frac {1}{m}[x^{(1)} dz^{(1)} + x^{(2)} dz^{(2)} +…+x^{(m)} dz^{(m)}]\\=\frac {1}{m}[x^{(1)}\quad x^{(2)}\quad…\quad x^{(m)}][dz^{(1)}\quad dz^{(2)}\quad…\quad dz^{(m)}]^T\\=\frac {1}{m}X(dZ)^T$

求取 db：

$db=\frac {1}{m} \sum\limits _{i=1}^{m} dz^{(i)}=\frac {1}{m}$ np.sum(dZ)

总结

$Z = w^TX + b = np.dot(w.T, X)+b\\A = \sigma (Z)\\dZ=A-Y\\db=\frac {1}{m}np.sum(dZ)\\dw= \frac{1}{m}X(dZ)^T=\frac{1}{m}np.dot(X, dZ.T)\\w:=w-\alpha dw\\b:=b-\alpha db$

Python中的广播（broadcasting）

若拿一个（m，n）的矩阵加减乘除另一个（1，n）的向量，这个向量会复制多次自动拓展成一个（m，n）的矩阵然后逐元素进行运算
若拿一个（m，1）的向量加减乘除另一个实数R，这个实数会复制多次自动拓展成一个（m，1）的向量然后逐元素进行运算
更多广播功能见 numpy 相关文档

在使用 numpy 时的注意事项

例子

错误的

>>import numpy as np
>>a = np.random.randn(5)#产生5个高斯随机变量并存在数组里
>>print(a)
[1.37838388  0.53281963 -0.41769013  0.69356822 -0.30333514]
>>print(a.shape)#输出 a 的形状
(5,)
>>print(a.T)#输出 a 的转置
[1.37838388  0.53281963 -0.41769013  0.69356822 -0.30333514]
>>print(np.dot(a,a.T))#输出a 和 a 的转置的点乘
8.65042528221

正确的

>>a = np.random.randn(5,1)
>>print(a)
[[-0.4593413 ]
 [-0.54494632]
 [-0.9348879 ]
 [-0.51491905]
 [ 0.91934378]]
>>print(a.T)
[[-0.4593413  -0.54494632 -0.9348879  -0.51491905  0.91934378]]
>>print(np.dot(a,a.T))
[[ 0.21099443  0.25031635  0.42943262  0.23652358 -0.42229257]
 [ 0.25031635  0.29696649  0.50946372  0.28060324 -0.50099301]
 [ 0.42943262  0.50946372  0.87401539  0.48139159 -0.85948338]
 [ 0.23652358  0.28060324  0.48139159  0.26514163 -0.47338763]
 [-0.42229257 -0.50099301 -0.85948338 -0.47338763  0.84519299]]

错误的例子在于 a = np.random.randn(5) 生成了一个形状为 (5,) 的名为 “秩为1的数组” ，而不是一个向量，这种数组转置之后显示完全一样，但是性质与向量不同，所以极易造成许多奇怪的 bug，所以要杜绝秩为1的数组的使用，而是使用 a = np.random.randn(5,1) 或者 a = np.random.randn(1,5)

减少错误的技巧

不要使用 秩为1的数组，始终使用（n，1）列向量或者（1，n）的行向量，例如：
1
a = np.random.randn(5,1)
经常使用断言语句来确保是向量而不是秩为1的数组,例如：
1
assert(a.shape == (5,1))

经常使用 reshape 语句 来确保矩阵和向量是需要的维度，例如：

1 2	a = np.random.randn(5)#产生了一个秩为1矩阵 a = a.reshape((5,1))#将其变为（5，1）的列向量